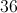Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Exponents

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : How To Multiply Complex Numbers

Evaluate:

$i^{-31}$

Possible Answers:

The expression is undefined

Correct answer:

Explanation:

$a^{-m}$ is defined to be equal to $\frac{1}{a^{m}}$ for any real or imaginary and for any real ; therefore,

$i^{-31} = \frac{1}{i^{31}}$

To evaluate a positive power of , divide the power by 4 and note the remainder:

$31 \div 4= 7 \textrm{ R }3$

Therefore,

$i ^{31} = i ^{3} = -i$

Substituting,

$i^{-31} = \frac{1}{-i}$

Rationalizing the denominator by multiplying both numerator and denominator by :

$i^{-31} = \frac{1 \cdot i}{-i \cdot i }= \frac{ i}{-i ^{2}}= \frac{ i}{-(-1)}= \frac{ i}{1}= i$

Report an Error

Example Question #1 : How To Find An Exponent From A Rational Number

Solve for .

$2^{x}= 64$

Possible Answers:

x=-6

x=64

x=5

x=6

$x=64^{2}$

Correct answer:

x=6

Explanation:

Since $2^{x}= 2^{6}$

Hence x=6

Report an Error

Example Question #1 : How To Find An Exponent From A Rational Number

Simplify:

$\sqrt[3]{x^{10}y^{8}z^{9}}$

Possible Answers:

$x^{3}y^{3}z^{3}$

$\sqrt[3]{xy^{2}}$

$x^{3}y^{2}z^{3}^{\sqrt[3]{xyz}}$

$x^{3}y^{2}z^{3}\sqrt[3]{xy^{2}}$

$x^{3}y^{2}z^{3}$

Correct answer:

$x^{3}y^{2}z^{3}\sqrt[3]{xy^{2}}$

Explanation:

$\sqrt[3]{x^{9}xy^{6}y^{2}z^{9}}=x^{3}y^{2}z^{3}\sqrt[3]{xy^{2}}$

Report an Error

Example Question #1 : How To Find An Exponent From A Rational Number

Solve for :

$\sqrt{x} -1= 4$

Possible Answers:

Correct answer:

Explanation:

From the equation one can see that

$\sqrt{x} = 5$

Hence must be equal to 25.

Report an Error

Example Question #2 : How To Find An Exponent From A Rational Number

Evaluate:

$\log 0.1=$

Possible Answers:

$\frac{1}{10}$

Correct answer:

Explanation:

$0.1= 10^{-1}$

$\log 0.1=-1$

Report an Error

Example Question #1 : How To Find An Exponent From A Rational Number

Solve for .

$\log_{2}x=4$

Possible Answers:

Correct answer:

Explanation:

$x= 2^4{}= 16$

Report an Error

Example Question #3 : How To Find An Exponent From A Rational Number

$\log 3=a$

and

$\log 5=b$

Find $\log 15$

Possible Answers:

a+b

$b^{2}$

$a^{2}$

Correct answer:

a+b

Explanation:

$\log 15=\log (5\cdot 3)=\log 5+\log 3$

Hence the correct answer is a+b .

Report an Error

Example Question #2 : Exponents And Rational Numbers

Solve for .

$\log (x+3)+\log x=1$

Possible Answers:

$5\ or\ -2$

$-5\ or\ 2$

Correct answer:

Explanation:

Use the rules of logarithms to combine terms.

$\log (x(x+3))=1$

Hence, $x(x+3)=10^{1}$

$x^{2}+3x=10$

x^2+3x-10=0

By fatoring we get (x+5)(x-2)=0

Hence $x=-5\ or\ 2$ .

However, you cannot take the logarithm of a negative number. Thus, the only value for is .

Report an Error

Example Question #4 : How To Find An Exponent From A Rational Number

If a piece of pie is cut into 3 sections, and each of those pieces is further cut into three sections, then those pieces are cut into three sections, how many (tiny) pieces of pie are there?

Possible Answers:

125

Correct answer:

Explanation:

The answer is 3³ = 27

Report an Error

Example Question #11 : Exponential Ratios And Rational Numbers

Solve for .

$\log _{9}x=\frac{1}{2}$

Possible Answers:

Correct answer:

Explanation:

$\log _{9}x=\frac{1}{2}$

$x = 9^{\frac{1}{2}}= 3$

Report an Error

View SAT Mathematics Tutors

Troy
Certified Tutor

Rice University, Bachelor in Arts, Kinesiology.

View SAT Mathematics Tutors

Priyanka
Certified Tutor

CUNY Hunter College, Bachelor in Arts, Economics.

View SAT Mathematics Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in Los Angeles, GRE Courses & Classes in Boston, GRE Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Washington DC, ACT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in San Diego, LSAT Courses & Classes in Atlanta, SAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Washington DC

Popular Test Prep

GRE Test Prep in Philadelphia, GMAT Test Prep in Miami, GRE Test Prep in Atlanta, GRE Test Prep in Washington DC, ACT Test Prep in Washington DC, ISEE Test Prep in San Diego, GRE Test Prep in Phoenix, ISEE Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Exponents

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #21 : How To Multiply Complex Numbers

Example Question #1 : How To Find An Exponent From A Rational Number

Example Question #1 : How To Find An Exponent From A Rational Number

Example Question #1 : How To Find An Exponent From A Rational Number

Example Question #2 : How To Find An Exponent From A Rational Number

Example Question #1 : How To Find An Exponent From A Rational Number

Example Question #3 : How To Find An Exponent From A Rational Number

Example Question #2 : Exponents And Rational Numbers

Example Question #4 : How To Find An Exponent From A Rational Number

Example Question #11 : Exponential Ratios And Rational Numbers

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: