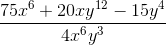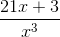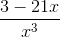The procedure for multplying together two rational expressions is the same as multiplying together any two fractions: find the product of the numerators and the product of the denominators separately, and then simplify the resulting quotient as far as possible, as shown:

\(\displaystyle \frac{15x^2+4xy^3-3y}{x^2y^7}\times\frac{5y^4}{4x^3}\)

\(\displaystyle =\frac{(15x^2+4xy^3-3y)(5y^4)}{(x^2y^7)(4x^3)}\)

\(\displaystyle =\frac{75x^2y^4+20xy^7-15y^5}{4x^5y^7}\)

\(\displaystyle =\frac{75x^2+20xy^3-15y}{4x^5y^3}\)

Since both expressions have a common denominator, x², we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.

Since both fractions in the expression have a common denominator of \(\displaystyle x^{2}\), we can combine like terms into a single numerator over the denominator:

\(\displaystyle \frac{7x-18}{x^{2}}+\frac{6x-14}{x^{2}}\)

\(\displaystyle =\frac{(7x-18)+(6x-14)}{x^{2}}\)

\(\displaystyle =\frac{13x-32}{x^{2}}\)

Since both rational terms in the expression have the common denominator \(\displaystyle 2x^{2}\), combine the numerators and simplify like terms:

\(\displaystyle \frac{5x-5}{2x^{2}} + \frac{7x+9}{2x^{2}}\)

\(\displaystyle =\frac{(5x-5)+(7x+9)}{2x^{2}}\)

\(\displaystyle =\frac{12x+4}{2x^{2}}\)

\(\displaystyle =\frac{6x+2}{x^2}\)

Since both terms in the expression have the common denominator \(\displaystyle x^{3}\), combine the fractions and simplify the numerators:

\(\displaystyle \frac{10x-9}{x^{3}}+\frac{11x+12}{x^{3}}\)

\(\displaystyle =\frac{(10x-9)+(11x+12)}{x^{3}}\)

\(\displaystyle =\frac{21x+3}{x^{3}}\)

There are a few ways to do this problem, but we will focus on the total number of votes method as follows. First, let Clinton = C, Gore = G, Paul = P, and Johnson = J. We know C + G + P + J = 150 million. We also know that C = 3J. Paul received 30% of the vote which is 150,000,000 * .3 = 45 million votes. Gore received 30 million votes. We can now create an equation with individual totals and substitute 3J for Clinton's vote total:

3J + 30 million + 45 million + J = 150 million

4J = 75 million

J = 18.75 million

Then C = 3J = 56.25 million. So Clinton received 56.25 million votes, Paul received 45 million votes, Gore received 30 million votes, and Johnson received 18.75 million votes.  The correct answer is Hillary Clinton.

Find how many free throws Justin made:  84 x 0.619 = 51.99.  Since the problem talks free throws, we round to 52 shots went in.  To calculate shots missed:

84 – 52 = 32.

Combine like terms by subtracting 6 from both sides so:  5x + 24 = –7x.  Then subtract 5x from both sides:  24 = –12x.  Divide both sides by –12 and x = –2.

ab - bc + d = d² - c²

We need to substitute values in for b, c, and d, and then solve the equation for a.

a(2) - 2(-1) + 0 = 0² - (-1)²

2a +2 + 0 = 0 - (1)

2a + 2 = -1

2a = -3

a = -3/2

The answer is -3/2.

First solve for x. The first equation would simplify as:

16 = 8x

x = 2

If we plug x = 2 into the second expression:

2(2) – 4 = 0 

0 is the correct answer.