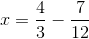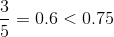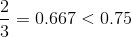All SAT Math Resources
Example Questions
Example Question #611 : Arithmetic
Evaluate the following:
None of the available answers
First we will evaluate the terms in the parentheses:
Next, we will square the first fraction:
We can evaluate the division as such:
Example Question #1492 : Sat Mathematics
Evaluate the expression:
When dividing fractions, you invert the second term and multiply the numbers.

You can reduce the numbers that are diagonal from each other to make the numbers smaller and easier to multiply.
Example Question #1491 : Sat Mathematics
Simplify
Fractions with variables cannot be divided
When you dividing fractions, multiply by the reciprocal of the denominator.
Example Question #1 : How To Subtract Fractions
Which fraction has a value greater than that of X?
First, start by putting changing the fractions in the equation so that they have the same denominator.
Then, you can easily subtract the numerators. The denominator stays the same at this point:
At this point, you can reduce the fraction by dividing the numerator and the denominator by 
Then, to easily compare the fraction to the answer choices, you can change the fraction to a decimal:
By changing the answer choices to decimals as well, you can easily figure out which value is greater than 
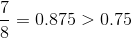

Example Question #1 : How To Add Fractions
Jesse has a large movie collection containing X movies. 1/3 of his movies are action movies, 3/5 of the remainder are comedies, and the rest are historical movies. How many historical movies does Jesse own?
(7/12)*X
(2/5)*X
(4/15)*X
(11/15)*X
(3/9)*X
(4/15)*X
1/3 of the movies are action movies. 3/5 of 2/3 of the movies are comedies, or (3/5)*(2/3), or 6/15. Combining the comedies and the action movies (1/3 or 5/15), we get 11/15 of the movies being either action or comedy. Thus, 4/15 of the movies remain and all of them have to be historical.
Example Question #122 : Fractions
If x = 1/3 and y = 1/2, find the value of 2x + 3y.
1
6/5
13/6
5/6
2
13/6
Substitute the values of x and y into the given expression:
2(1/3) + 3(1/2)
= 2/3 + 3/2
= 4/6 + 9/6
= 13/6
Example Question #3 : How To Add Fractions
Example Question #612 : Arithmetic
What is the solution, reduced to its simplest form, for 
Example Question #152 : Fractions
What is the result of adding 


Let us first get our value for the percentage of the first fraction. 20% of 2/7 is found by multiplying 2/7 by 2/10 (or, simplified, 1/5): (2/7) * (1/5) = (2/35)
Our addition is therefore (2/35) + (1/4). There are no common factors, so the least common denominator will be 35 * 4 or 140. Multiply the numerator and denominator of 2/35 by 4/4 and the numerator of 1/4 by 35/35.
This yields:
(8/140) + (35/140) = 43/140, which cannot be reduced.
Example Question #613 : Arithmetic
Add:
Find the least common denominator to solve this problem
Multiply 27 with 

Convert the fractions.
Combine the terms as one fraction.
The answer is:
Certified Tutor
All SAT Math Resources