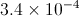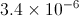We replace 8 with 2³ so that each term has the same base, making the equation 2³ 2^x = 2^y. The terms on the left now have the same base, so we add the exponents to get 2^3+x = 2^y. Taking the log₂ of each side gives 3 + x = y, and therefore x = y – 3.

\(\displaystyle \dpi{100} \small 256,000,000,000 = 2.56\times 10^{11}\) 

The exponent is equal to the number of decimal points shifted.

In this case the exponent is positive hence you have to move the decimal point 4 places to the right from where it is in the problem giving us

\(\displaystyle 23,000\)

In this case you have to move the decimal point 6 places to the right. When you move the decimal point to the right the exponent becomes negative.  Similarly when you move the decimal point to the left the exponent is positive.  Also, to the left of the decimal place there can be only one digit.

\(\displaystyle 3.4* 10^{-6}\)

First, when we round to the nearest thousand we get 5, 679, 000 since we round up when the next digit is greater than 5.

Then, to put it in scientific notation, we arrange the digits so that a decimal point creates a number between 1 and 10. We get 5.679.

Then, we want the exponent of the 10 to be the number of times the decimal needs to move to the right. This is 6 times.

Thus, we get our answer. \(\displaystyle 5.679 \times 10^6\) 

In order to write a number in scientific notation, you must shift the number of decimal places to get a number in the ones place.

Since the original number is a decimal, the exponent will need to be negative. This eliminates three answer choices. 

In order to get \(\displaystyle 0.000000537\) into scientific notation with '5' in the ones place, you must shift the decimal over seven places.

Therefore, the final answer in scientific notation is \(\displaystyle 5.37 \times 10^{-7}\).

In scientific notation, we want one digit in the unit's place, followed by a decimal point and subsequent digits.

The exponent of 10 is the number of units the decimal point has been shifted. 

For 0.00000956, we want to move the decimal over so that we get the number 9.56 times 10 to some power. To do this, we must move the decimal over 6 places. Since 0.00000956 is obviously smaller than 9.56, that means that our exponent must be negative. 

Therefore, our answer is \(\displaystyle 9.56 \cdot 10^{-6}\). 

To expand our number, we should look at the exponent provided. We see that our exponent raises \(\displaystyle 10\) to the power of positive \(\displaystyle 5\). Since the exponent is positive, we know that we need to move our decimal to the right five places. Doing that yields our answer, \(\displaystyle 620,000\). 

To put a number in scientific notation, we want to have a number with one digit in the units place followed by a decimal point and any subsequent digits. That number is then multiplied by ten raised to a power that matches how many places we moved the decimal point in the original number. 

To write this number in scientific notation, we want our expression to be \(\displaystyle 6.7 \cdot 10^x\). When we move the decimal place to the left in \(\displaystyle 6,700,000\) to create \(\displaystyle 6.7\), we move it six places to the left. 

Therefore, this number in scientific notation is \(\displaystyle 6.7 \cdot 10^6\).

Which of the following is equivalent to \(\displaystyle 5.673*10^{-3}\)?

To solve this problem, all we need to do is move the decimal point.

Because we have a negative exponent (-3), we have to move our decimal point to the left.

Because our exponent is 3, we will move the decimal point 3 to the left:

\(\displaystyle 0005.673*10^{-3}=0.005673\)

Making our answer:

\(\displaystyle 0.005673\)