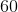Since v is divisible by 2, 3 and 15, v must be a multiple of 30. Any number that is divisible by both 2 and 15 must be divisible by their product, 30, since this is the least common multiple.

Out of all the answer choices, v + 30 is the only one that equals a multiple of 30.

We are given information that m/4 is 10 greater than m/3. We set up an equation where m/4 = m/3 + 10.

We must then give the m variables a common denominator in order to solve for m. Since 3 * 4 = 12, we can use 12 as our denominator for both m variables.

m/4 = m/3 + 10 (Multiply m/4 by 3 in the numerator and denominator.)

3m/12 = m/3 + 10 (Multiply m/3 by 4 in the numerator and denominator.)

3m/12 = 4m/12 + 10 (Subtract 4m/12 on both sides.)

-m/12 = 10 (Multiply both sides by -12.)

m = -120

-120/4 = -30 and -120/3 = -40. -30 is 10 greater than -40.

The greatest common divisor of $\displaystyle x$ and $\displaystyle y$ is 10. This means that the prime factorizations of $\displaystyle x$ and $\displaystyle y$ must both contain a 2 and a 5. 

The greatest common divisor of $\displaystyle y$ and $\displaystyle z$ is 9. This means that the prime factorizations of $\displaystyle y$ and $\displaystyle z$ must both contain two 3's.

The greatest common divisor of $\displaystyle x$ and $\displaystyle z$ is 8. This means that the prime factorizations of $\displaystyle x$ and $\displaystyle z$ must both contain three 2's.

Thus:

$\displaystyle x=2^3*5*A,\ y=2*3^2*5*B,\ z=2^3*3^2*C$

We substitute these equalities into the given expression and simplify.

$\displaystyle \frac{yz}{x}=\frac{(2*3^2*5*B)(2^3*3^2*C)}{(2^3*5*A)} = \frac{162BC}{A}$

Since $\displaystyle y$ and $\displaystyle z$ are two-digit integers (equal to $\displaystyle 90B$ and $\displaystyle 72C$respectively), we must have $\displaystyle B=1$ and $\displaystyle C=1$. Any other factor values for $\displaystyle B$ or $\displaystyle C$ will produce three-digit integers (or greater).

$\displaystyle x$ is equal to $\displaystyle 40A$, so $\displaystyle A$ could be either 1 or 2. 

Therefore:

$\displaystyle \frac{yz}{x}=162$

or 

$\displaystyle \frac{yz}{x}=81$

Greatest common factor is a common factor shared by two or more numbers. Both numbers are even, so let's divide both numbers by two. We get $\displaystyle 2, 3$. These are prime numbers (factors of one and itsef) in which we are done. Anytime we have two prime numbers or one prime and one composite number, we are finished. So the greatest common factor is $\displaystyle 2$.

Greatest common factor is a common factor shared by two or more numbers. $\displaystyle 8$ is a multiple of $\displaystyle 4$, so let's divide $\displaystyle 4$ for both numbers. We get $\displaystyle 1, 2$. We are finished as these are the basic numbers. So the greatest common factor is $\displaystyle 4$.

Greatest common factor is a common factor shared by two or more numbers. $\displaystyle 19$ is a prime number. $\displaystyle 27$ is a composite number. Since we have a prime and composite number, the greatest common factor is $\displaystyle 1$. 

Greatest common factor is a common factor shared by two or more numbers. Both numbers are even, so let's divide two for both numbers. We get $\displaystyle 12, 37$.  We have  one prime and one composite number, so we are finished. The greatest common factor is $\displaystyle 2$.

Greatest common factor is a common factor shared by two or more numbers. If you know the divisibility rule of $\displaystyle 9$ (sum of digits are divisible by $\displaystyle 9$), then the answer is just $\displaystyle 9$ as the quotient is $\displaystyle 2\textup{ and } 27$. We have a prime and composite number. However, if you don't and only know the divisibility rule of $\displaystyle 3$, then we can divide both numbers by $\displaystyle 3$ to get $\displaystyle 6, 81$. We do it once more to get $\displaystyle 2, 27$. Since we divided twice by $\displaystyle 3$, we multiply these factors and this is our greatest common factor of $\displaystyle 18, 243$. Our answer is $\displaystyle 9$.

Greatest common factor is a common factor shared by two or more numbers. If you know divisibility rule of $\displaystyle 11$, then this is the answer. However, this isn't easy to spot, so we will do process of elimination. The numbers are odd and if we have even factors, we never generate odd numbers so $\displaystyle 22$ is wrong. Next, check divisibility rule of $\displaystyle 3$. The digits of $\displaystyle 121$ add to $\displaystyle 4$ which isn't divisible by $\displaystyle 3$ so $\displaystyle 3$ is wrong. Next, let's divide $\displaystyle 33$ into $\displaystyle 121$. We get a decimal value and that's wrong since if we consider $\displaystyle 121$ to be a multiple of $\displaystyle 33$, it should be a whole number and not a decimal. Finally, by dividing $\displaystyle 121$ and $\displaystyle 11$, it's also $\displaystyle 11$. This is our answer. To find out if $\displaystyle 121$ is divisible by $\displaystyle 11$, just add the outside digits and match the middle one. Since it does, $\displaystyle 121$ is divisible by $\displaystyle 11$.

These two numbers are definitely divisible by $\displaystyle 5$. When we divide both numbers by $\displaystyle 5$, we get $\displaystyle 11$ and $\displaystyle 16$ remaining. Since we have a combination of a prime and composite number, then we can't find any more factors. Our answer is $\displaystyle 5$.