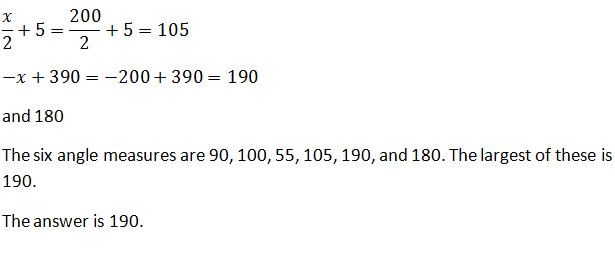All SAT Math Resources
Example Questions
Example Question #21 : Geometry
Possible Answers:
170
210
200
180
190
Example Question #1 : Hexagons
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
Possible Answers:
Correct answer:
Explanation:
The sum of the interior angles of a polygon is given by 

Example Question #1 : Hexagons
Find the sum of all the inner angles in a hexagon.
Possible Answers:
Correct answer:
Explanation:
To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,
All SAT Math Resources
SAT Math Tutors in Top Cities:
Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors
Popular Courses & Classes
GRE Courses & Classes in Denver, GRE Courses & Classes in Washington DC, ACT Courses & Classes in New York City, ISEE Courses & Classes in Denver, ACT Courses & Classes in Chicago, ACT Courses & Classes in Miami, SSAT Courses & Classes in New York City, MCAT Courses & Classes in Seattle, MCAT Courses & Classes in Phoenix, SSAT Courses & Classes in Houston
Popular Test Prep
SAT Test Prep in Atlanta, ACT Test Prep in New York City, GMAT Test Prep in Boston, GMAT Test Prep in San Diego, MCAT Test Prep in Washington DC, SSAT Test Prep in Phoenix, LSAT Test Prep in Los Angeles, SSAT Test Prep in Philadelphia, SSAT Test Prep in Denver, GRE Test Prep in Seattle