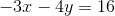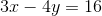Equation of line: \(\displaystyle \small y = mx+b\),   \(\displaystyle \small m\) = slope, \(\displaystyle \small b\) = \(\displaystyle y\)-intercept

Step 1) Find slope (\(\displaystyle \small m\)):  rise/run    \(\displaystyle \small \frac{8-2}{3-1}=\frac{6}{2}=3\)

Step 2) Find \(\displaystyle y\)-intercept (\(\displaystyle \small b\)):   \(\displaystyle \small \frac{2-b}{1-0}=3\) 

                                                      \(\displaystyle \small 2-b = 3\)

                                                      \(\displaystyle \small 2 = 3 + b\)

                                                       \(\displaystyle \small -1 =b\)

\(\displaystyle \small y=3x-1\)

Let \(\displaystyle P_{1}=(1,3)\) and \(\displaystyle P_{2}=(7,5)\)

The slope is geven by:  \(\displaystyle m = (y_{2} - y_{1}) \div (x_{2} - x_{1})\)  so

\(\displaystyle m=\frac{1}{3}\)

Then we use the slope-intercept form of an equation;  \(\displaystyle y=mx+b\) so

\(\displaystyle b=\frac{8}{3}\)

And we convert 

\(\displaystyle y=\frac{1}{3}x+\frac{8}{3}\) 

to standard form.

In order to find the equation of the line, we will first need to find the slope between the two points through which it passes. The slope, \(\displaystyle m\), of a line that passes through the points \(\displaystyle (x_1,y_1)\) and \(\displaystyle (x_2,y_2)\) is given by the formula below:

\(\displaystyle \text{slope}=m=\frac{y_2-y_1}{x_2-x_1}\)

We are given our two points, (4,7) and (8,10), allowing us to calculate the slope.

\(\displaystyle m=\frac{10-7}{8-4}=\frac{3}{4}\)

Next, we can use point slope form to find the equation of a line with this slope that passes through one of the given points. We will use (4,7).

\(\displaystyle y-y_1=m(x-x_1)\)

\(\displaystyle y-7=\frac{3}{4}(x-4)\)

Multiply both sides by four to eliminate the fraction, and simplify by distribution.

\(\displaystyle 4(y-7)=4(\frac{3}{4})(x-4)\)

\(\displaystyle 4y-28=3(x-4)\)

\(\displaystyle 4y-28=3x-12\)

Subtract \(\displaystyle 4y\) from both sides and add twelve to both sides.

\(\displaystyle -28=3x-4y-12\)

\(\displaystyle -16=3x-4y\)

This gives our final answer: \(\displaystyle 3x-4y=-16\)

First, solve for slope.

\(\displaystyle \small m=\frac{\Delta y}{\Delta x}=\frac{2-4}{6-(-2)}=\frac{-2}{8}=-\frac{1}{4}\)

Then, substitute one of the points into the equation y=mx+b.

\(\displaystyle \small 2=(-\frac{1}{4})(6)+b\)

\(\displaystyle \small 2=(-\frac{3}{2})+b\)

\(\displaystyle \small b=2+\frac{3}{2}=\frac{7}{2}\)

This leaves us with the equation \(\displaystyle \small y=-\frac{1}{4}+\frac{7}{2}\)

To solve this question, you could use two points such as (1.2,0) and (0,-4) to calculate the slope which is 10/3 and then read the y-intercept off the graph, which is -4.

P₁ (0, 6) and P₂ (4, 0)

First, calculate the slope:  m = rise ÷ run = (y₂ – y₁)/(x₂ – x₁), so m = –3/2

Second, plug the slope and one point into the slope-intercept formula: 

y = mx + b, so 0 = –3/2(4) + b and b = 6

Thus, y = –3/2x + 6

If P₁(1, 3) and P₂(3, 6), then calculate the slope by m = rise/run = (y₂ – y₁)/(x₂ – x₁) = 3/2

Use the slope and one point to calculate the intercept using y = mx + b

Then convert the slope-intercept form into standard form.

The slope intercept form states that \(\displaystyle \dpi{100} \small y=mx+b\). In order to convert the equation to the slope intercept form, isolate \(\displaystyle \dpi{100} \small y\) on the left side:

\(\displaystyle \dpi{100} \small 8x-2y=12\)

\(\displaystyle \dpi{100} \small -2y=-8x+12\)

\(\displaystyle \dpi{100} \small y=4x-6\)

The equation of a line is

y=mx + b where m is the slope

Rearrange the equation to match this:

7x + 28y = 84

28y = -7x + 84

y = -(7/28)x + 84/28

y = -(1/4)x + 3

m = -1/4

First solve for the slope of the line, m using y=mx+b

m = (y2 – y1) / (x2 – x1)

= (15 – 14) / (–5 –3)

= (1 )/( –8)

=–1/8

y = –(1/8)x + b

Now, choose one of the coordinates and solve for b:

14 = –(1/8)3 + b

14 = –3/8 + b

b = 14 + (3/8)

b = 14.375

y = –(1/8)x + 14.375