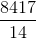Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #6 : How To Evaluate A Fraction

If 5x=55 , x+y = 23 , and y-z=2 , find the value of $\frac{2x+y}{z}$ .

Possible Answers:

$\frac{17}{5}$

$\frac{9}{2}$

$\frac{19}{5}$

$\frac{13}{5}$

$\frac{16}{7}$

Correct answer:

$\frac{17}{5}$

Explanation:

In order to solve $\frac{2x+y}{z}$ , we must first find the values of , , and using the initial equations provided. Starting with 5x=55 :

$x=\frac{55}{5}=11$

Then:

x+y=23

11+y=23

y=12

Finally:

y-z=2

12-z=2

10=z

With the values of , , and in hand, we can solve the final equation:

$\frac{2x+y}{z}$

$=\frac{2(11)+12}{10}$

$=\frac{22+12}{10}$

$=\frac{34}{10}$

$=\frac{17}{5}$

Report an Error

Example Question #7 : How To Evaluate A Fraction

If $x =\frac{1}{2}$ and $y=\frac{2}{3}$ , then which of the following is equal to $\frac{2}{x+y}$ ?

Possible Answers:

$\frac{10}{3}$

$\frac{12}{7}$

$\frac{9}{7}$

$2 \frac{1}{3}$

Correct answer:

$\frac{12}{7}$

Explanation:

In order to solve $\frac{2}{x+y}$ , first substitute the values of and provided in the problem:

$\frac{2}{\frac{1}{2}+\frac{2}{3}}$

Find the Least Common Multiple (LCM) of the fractional terms in the denominator and find the equivalent fractions with the same common denominator:

$\frac{2}{\frac{1}{2}+\frac{2}{3}}$

$=\frac{2}{\frac{3}{6}+\frac{4}{6}}$

$=\frac{2}{\frac{7}{6}}$

Finally, in order to divide by a fraction, we must multiply by the reciprocal of the fraction:

$=2\times \frac{6}{7}$

$=\frac{12}{7}$

Report an Error

Example Question #8 : How To Evaluate A Fraction

Find the value of if $w=\bigg(\frac{1}{3}+y\bigg)^{2}$ and $y=\frac{1}{9}$ .

Possible Answers:

$\frac{9}{10}$

$\frac{16}{81}$

$\frac{3}{55}$

$\frac{4}{27}$

$\frac{1}{12}$

Correct answer:

$\frac{16}{81}$

Explanation:

In order to solve for , first substitute $y=\frac{1}{9}$ into the equation for :

$w=\bigg(\frac{1}{3}+y\bigg)^{2}$

$w=\bigg(\frac{1}{3}+\frac{1}{9}\bigg)^{2}$

Then, find the Least Common Multiple (LCM) of the two fractions and generate equivalent fractions with the same denominator:

$w=\bigg(\frac{3}{9}+\frac{1}{9}\bigg)^{2}$

Finally, simplify the equation:

$w=\bigg(\frac{4}{9}\bigg)^{2}$

$w=\frac{16}{81}$

Report an Error

Example Question #2 : How To Evaluate A Fraction

$\frac{7^{12}-7^{10}}{7^{11}-7^{9}}=$

Possible Answers:

343

Correct answer:

Explanation:

Factor out 7 from the numerator: $\frac{7(7^{11}-7^{9})}{7^{11}-7^{9}}$

This simplifies to 7.

Report an Error

Example Question #11 : How To Evaluate A Fraction

If pizzas cost dollars and sodas cost dollars, what is the cost of pizzas and sodas in terms of and ?

Possible Answers:

$5x+\frac{3y}{15}$

$\frac{3x+5y}{15}$

15xy

3x+5y

15x+5y

Correct answer:

$\frac{3x+5y}{15}$

Explanation:

If 10 pizzas cost x dollars, then each pizza costs x/10. Similarly, each soda costs y/6. We can add the pizzas and sodas together by finding a common denominator:

$2*\frac{x}{10}+2*\frac{y}{6}=\frac{x}{5}+\frac{y}{3}=\frac{3x}{3*5}+\frac{5y}{5*3}=\frac{3x+5y}{15}$

Report an Error

Example Question #12 : How To Evaluate A Fraction

Gre9

According the pie chart, the degree measure of the sector representing the number of workers spending 5 to 9 years in the same role is how much greater in the construction industry chart than in the financial industry chart?

Possible Answers:

$70^{\circ}$

$7^{\circ}$

$18^{\circ}$

$25^{\circ}$

$35^{\circ}$

Correct answer:

$25^{\circ}$

Explanation:

Since the values in the pie charts are currently in terms of percentages (/100), we must convert them to degrees (/360, since within a circle) to solve the question. The "5 to 9 years" portion for the financial and construction industries are 18 and 25 percent, respectively. As such, we can cross-multiply both:

18/100 = x/360

x = 65 degrees

25/100 = y/360

y = 90 degrees

Subtract: 90 – 65 = 25 degrees

Alternatively, we could first subtract the percentages (25 – 18 = 7), then convert the 7% to degree form via the same method of cross-multiplication.

Report an Error

Example Question #871 : Algebra

6 contestants have an equal chance of winning a game. One contestant is disqualified, so now the 5 remaining contestants again have an equal chance of winning. How much more likely is a contestant to win after the disqualification?

Possible Answers:

$\frac{1}{6}$

$\frac{1}{2}$

$\frac{2}{5}$

$\frac{1}{5}$

$\frac{1}{30}$

Correct answer:

$\frac{1}{30}$

Explanation:

When there are 6 people playing, each contestant has a 1/6 chance of winning. After the disqualification, the remaining contestants have a 1/5 chance of winning.

1/5 – 1/6 = 6/30 – 5/30 = 1/30.

Report an Error

Example Question #15 : How To Evaluate A Fraction

Simplify:

$\frac{\frac{1}{4}+\frac{5}{7}}{\frac{2}{5}}$

Possible Answers:

$\frac{47}{5}$

$\frac{98}{71}$

$\frac{27}{70}$

$\frac{81}{7}$

$\frac{135}{56}$

Correct answer:

$\frac{135}{56}$

Explanation:

Begin by simplifying the numerator.

$\frac{1}{4}+\frac{5}{7}$ has a common denominator of . Therefore, we can rewrite it as:

$\frac{7}{28}+\frac{20}{28}=\frac{27}{28}$

Now, in our original problem this is really is:

$\frac{\frac{27}{28}}{\frac{2}{5}}$

When you divide by a fraction, you really multiply by the reciprocal:

$\frac{\frac{27}{28}}{\frac{2}{5}}=\frac{27}{28} \cdot\frac{5}{2}=\frac{135}{56}$

Report an Error

Example Question #261 : Gre Quantitative Reasoning

Simplify:

$\frac{\frac{81}{5}+\frac{7}{25}}{\frac{1}{9}-\frac{2}{7}}$

Possible Answers:

$-\frac{25956}{275}$

$\frac{8414}{41}$

$-\frac{4532}{1575}$

$\frac{8417}{14}$

$-\frac{551}{12}$

Correct answer:

$-\frac{25956}{275}$

Explanation:

Begin by simplifying the numerator and the denominator.

Numerator

$\frac{81}{5}+\frac{7}{25}$ has a common denominator of . Therefore, we have:

$\frac{405}{25}+\frac{7}{25} = \frac{412}{25}$

Denominator

$\frac{1}{9}-\frac{2}{7}$ has a common denominator of . Therefore, we have:

$\frac{7}{63}-\frac{18}{63}=-\frac{11}{63}$

Now, reconstructing our fraction, we have:

$\frac{\frac{412}{25}}{-\frac{11}{63}}$

To make this division work, you multiply the numerator by the reciprocal of the denominator:

$\frac{\frac{412}{25}}{-\frac{11}{63}} = \frac{412}{25} \cdot -\frac{63}{11} =-\frac{25956}{275}$

Report an Error

Example Question #872 : Algebra

Simplify: $(\frac{x-4}{0.5})\div (\frac{1}{x+4})$

Possible Answers:

2x^2-32

None of the other answer choices are correct.

$\frac{3}{2x^2}-16$

$\frac{1}{2}$

Correct answer:

2x^2-32

Explanation:

Recall that dividing is equivalent multiplying by the reciprocal. Therefore, ((x - 4) / (1 / 2)) / (1 / (x + 4)) = ((x - 4) * 2) * (x + 4) / 1.

Let's simplify this further:

(2x – 8) * (x + 4) = 2x² – 8x + 8x – 32 = 2x² – 32

Report an Error

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Christopher
Certified Tutor

Rose-Hulman Institute of Technology, Bachelor of Science, Physics. University of Washington, Master of Science, Physics.

View SAT Mathematics Tutors

Kenneth
Certified Tutor

North Georgia University, Bachelors, Accounting. Brenau University, Masters, Business.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SAT Courses & Classes in Denver, ACT Courses & Classes in Chicago, ACT Courses & Classes in Seattle, SAT Courses & Classes in Seattle, GMAT Courses & Classes in Seattle, GMAT Courses & Classes in Washington DC, ACT Courses & Classes in Philadelphia, SAT Courses & Classes in San Diego, GMAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Houston

Popular Test Prep

MCAT Test Prep in San Diego, ACT Test Prep in Chicago, ISEE Test Prep in Washington DC, GMAT Test Prep in Washington DC, LSAT Test Prep in Denver, GMAT Test Prep in Dallas Fort Worth, LSAT Test Prep in New York City, GRE Test Prep in Phoenix, ACT Test Prep in Philadelphia, SSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #6 : How To Evaluate A Fraction

Example Question #7 : How To Evaluate A Fraction

Example Question #8 : How To Evaluate A Fraction

Example Question #2 : How To Evaluate A Fraction

Example Question #11 : How To Evaluate A Fraction

Example Question #12 : How To Evaluate A Fraction

Example Question #871 : Algebra

Example Question #15 : How To Evaluate A Fraction

Example Question #261 : Gre Quantitative Reasoning

Example Question #872 : Algebra

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: