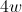All SSAT Middle Level Math Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A Rectangle
The width of a rectangle is half of its length. If the width is given as what is the perimeter of the rectangle in terms of ?
The sum of the widths is and since the width is half the length, each length is . Since there are 2 lengths we get a total perimeter of .
Example Question #102 : Geometry

The above figure shows the size and shape of a yard that is to be surrounded by some fence. How many feet of fence will be needed?
Note: all sides meet at right angles.
The best way to see that 750 feet of fence are needed is to look at this augmented diagram.
Note that two of the sides are extended to form a smaller rectangle whose sides can be deduced by subtraction. Since opposite sides of a rectangle are congruent, this allows us to fill in the two missing sidelengths of the original figure.

Now add:
Example Question #1 : How To Find The Perimeter Of A Rectangle

Give the perimeter of the rectangle in the above diagram.
The perimeter of a rectangle is the sum of the length and the width, multiplied by 2:
The rectangle has a perimeter of 38 centimeters.
Example Question #31 : Quadrilaterals

Give the perimeter of the rectangle in the above diagram.
The perimeter of a rectangle can be calculated by multiplying two by the sum of the length and width of the rectangle.
The perimeter of the rectangle is inches.
Example Question #2 : How To Find The Perimeter Of A Rectangle

Figure NOT drawn to scale.
Give the perimeter of the green polygon in the above figure.
The perimeter cannot be determined from the information given.
Since opposite sides of a rectangle have the same measure, the missing sidelengths can be calculated as in the diagram below:

The sidelengths of the green polygon can now be added to find the perimeter:
Example Question #71 : Plane Geometry
The width of a rectangle is one-third of its length. If the width is given as what is the perimeter of the rectangle in terms of ?
The perimeter of a rectangle is the sum of its sides.
The sum of the widths is and since the width is one-third of the length, each length is . Since there are lengths we get a total of . Widths + lengths =
Example Question #1 : How To Find The Perimeter Of The Rectangle
You are given equilateral triangle and Rectangle
with .
What is the perimeter of Rectangle ?
is equilateral, so .
Also, since opposite sides of a rectangle are congruent,
and
The perimeter of Rectangle is
Example Question #32 : Quadrilaterals
A hectare is a unit of area equal to 10,000 square meters.
A 150-hectare plot of land is rectangular and is 1.2 kilometers in width. Give the perimeter of this land.
150 hectares is equal to square meters.
The width of this land is 1.2 kilometers, or meters. Divide the area by the width to get:
meters
The perimeter of the land is
meters, or kilometers.
Example Question #1 : How To Find The Perimeter Of The Rectangle
The length of a rectangle is two times as long as the width. The width is equal to inches. What is the perimeter of the rectangle?
Example Question #2 : How To Find The Perimeter Of The Rectangle
How many meters of fence are needed to enclose a rectangular field that has a length of 1000 meters and a width of 100 meters?
The perimeter of a rectangle is simply the sum of the four sides:
All SSAT Middle Level Math Resources