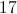We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Squares / Square Roots

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Squares / Square Roots

Evaluate:

$\sqrt{121} + \sqrt{49}$ $\displaystyle \sqrt{121} + \sqrt{49}$

Possible Answers:

$\displaystyle 17$

$\displaystyle 16$

$\displaystyle 15$

$\displaystyle 18$

$\displaystyle 14$

Correct answer:

$\displaystyle 18$

Explanation:

$11 ^{2 } = 11 \times 11 = 121$ $\displaystyle 11 ^{2 } = 11 \times 11 = 121$, so $\sqrt{121} = 11$ $\displaystyle \sqrt{121} = 11$.

$7 ^{2 } = 7 \times 7 = 49$ $\displaystyle 7 ^{2 } = 7 \times 7 = 49$, so $\sqrt{49} = 7$ $\displaystyle \sqrt{49} = 7$.

$\sqrt{121} + \sqrt{49} = 11 + 7 = 18$ $\displaystyle \sqrt{121} + \sqrt{49} = 11 + 7 = 18$

Report an Error

Example Question #12 : Squares / Square Roots

Let $N = \sqrt{7^{2}-5^{2}-3^{2}}$ $\displaystyle N = \sqrt{7^{2}-5^{2}-3^{2}}$

Then which of the following statements is correct?

Possible Answers:

$\displaystyle 3 < N < 4$

2< N <3 $\displaystyle 2< N < 3$

N = 3 $\displaystyle N = 3$

1< N <2 $\displaystyle 1< N < 2$

N = 2 $\displaystyle N = 2$

Correct answer:

$\displaystyle 3 < N < 4$

Explanation:

$N = \sqrt{7^{2}-5^{2}-3^{2}} = \sqrt{49-25-9} = \sqrt{24-9} = \sqrt{15}$ $\displaystyle N = \sqrt{7^{2}-5^{2}-3^{2}} = \sqrt{49-25-9} = \sqrt{24-9} = \sqrt{15}$

$\displaystyle 9 < 15 < 16$, so

$\sqrt{9} < \sqrt{15} < \sqrt{16}$ $\displaystyle \sqrt{9} < \sqrt{15} < \sqrt{16}$

$\displaystyle 3 < N < 4$

Report an Error

Example Question #11 : Squares / Square Roots

Let $N = \sqrt{10 \times 20 + 7 \times 8}$ $\displaystyle N = \sqrt{10 \times 20 + 7 \times 8}$

Which of the following is a true statement?

Possible Answers:

N = 16 $\displaystyle N = 16$

N = 14 $\displaystyle N = 14$

15 <N< 16 $\displaystyle 15 < N< 16$

14 <N< 15 $\displaystyle 14 < N< 15$

N = 15 $\displaystyle N = 15$

Correct answer:

N = 16 $\displaystyle N = 16$

Explanation:

$N = \sqrt{10 \times 20 + 7 \times 8}= \sqrt{200 + 56}= \sqrt{256}$ $\displaystyle N = \sqrt{10 \times 20 + 7 \times 8}= \sqrt{200 + 56}= \sqrt{256}$

Since $\displaystyle 16^2 = 256$, $N = \sqrt{256} = 16$ $\displaystyle N = \sqrt{256} = 16$

Report an Error

Example Question #14 : Squares / Square Roots

Which of the answer choices is equivalent to $2\sqrt{3}$ $\displaystyle 2\sqrt{3}$?

Possible Answers:

$\sqrt{36}$ $\displaystyle \sqrt{36}$

$\sqrt{6}$ $\displaystyle \sqrt{6}$

$\sqrt{12}$ $\displaystyle \sqrt{12}$

$\sqrt{9}$ $\displaystyle \sqrt{9}$

$\sqrt{18}$ $\displaystyle \sqrt{18}$

Correct answer:

$\sqrt{12}$ $\displaystyle \sqrt{12}$

Explanation:

$\displaystyle 2$ can also be written as $\sqrt{4}$ $\displaystyle \sqrt{4}$, so $2\sqrt{3}$ $\displaystyle 2\sqrt{3}$ can also be written as $\sqrt{4\cdot 3}$ $\displaystyle \sqrt{4\cdot 3}$, or $\sqrt{12}$ $\displaystyle \sqrt{12}$.

Report an Error

Example Question #12 : Squares / Square Roots

What is the square root of $\displaystyle 49$?

Possible Answers:

$\displaystyle 6$

$\displaystyle 98$

$\displaystyle 14$

$\displaystyle 7$

2401 $\displaystyle 2401$

Correct answer:

$\displaystyle 7$

Explanation:

The square root of $\displaystyle 49$ is $\displaystyle 7$, since $7\cdot7=49$ $\displaystyle 7\cdot7=49$.

Report an Error

Example Question #13 : How To Find The Square Root

Which of the answer choices is equivalent to $\sqrt{24}$ $\displaystyle \sqrt{24}$?

Possible Answers:

$\displaystyle 8$

$\displaystyle 12$

$\displaystyle 4$

$2\sqrt{4}$ $\displaystyle 2\sqrt{4}$

$2\sqrt{6}$ $\displaystyle 2\sqrt{6}$

Correct answer:

$2\sqrt{6}$ $\displaystyle 2\sqrt{6}$

Explanation:

Recognize that $\sqrt{24}=\sqrt{4\cdot 6}$ $\displaystyle \sqrt{24}=\sqrt{4\cdot 6}$. Since $\sqrt{4}=2$ $\displaystyle \sqrt{4}=2$, we can move the $\displaystyle 2$ outside of the radical sign. This leaves us with $2\sqrt{6}$ $\displaystyle 2\sqrt{6}$.

Report an Error

Example Question #13 : Squares / Square Roots

$x^{2} = 49, \left | x\right | + 7 = ?$ $\displaystyle x^{2} = 49, \left | x\right | + 7 = ?$

Possible Answers:

Correct answer:

Explanation:

If $x^{2} = 49$ $\displaystyle x^{2} = 49$, then $x=\pm 7$ $\displaystyle x=\pm 7$.

Therefore, $\left | x \right |+7=7+7=14$ $\displaystyle \left | x \right |+7=7+7=14$.

Report an Error

Example Question #14 : Squares / Square Roots

Evaluate:

$\sqrt{\frac{169}{100}}$ $\displaystyle \sqrt{\frac{169}{100}}$

Possible Answers:

$-\frac{10}{13}$ $\displaystyle -\frac{10}{13}$

$-\frac{13}{10}$ $\displaystyle -\frac{13}{10}$

$\frac{13}{10}$ $\displaystyle \frac{13}{10}$

$\frac{10}{13}$ $\displaystyle \frac{10}{13}$

$\sqrt{\frac{169}{100}}$ $\displaystyle \sqrt{\frac{169}{100}}$ is undefined.

Correct answer:

$\frac{13}{10}$ $\displaystyle \frac{13}{10}$

Explanation:

To find the square root of a fraction, extract the square root of both the numerator and the denominator. Since $10 ^{2} = 10 \times 10 = 100$ $\displaystyle 10 ^{2} = 10 \times 10 = 100$, $\sqrt{100} = 10$ $\displaystyle \sqrt{100} = 10$, and since $13^{2} = 169$ $\displaystyle 13^{2} = 169$, $\sqrt{169} = 13$ $\displaystyle \sqrt{169} = 13$.

Combine these results:

$\sqrt{\frac{169}{100}} = \frac{\sqrt{169}}{\sqrt{100}} = \frac{13}{10}$ $\displaystyle \sqrt{\frac{169}{100}} = \frac{\sqrt{169}}{\sqrt{100}} = \frac{13}{10}$

Report an Error

Example Question #15 : Squares / Square Roots

Evaluate:

$\sqrt{0.0009}$ $\displaystyle \sqrt{0.0009}$

Possible Answers:

0.00003 $\displaystyle 0.00003$

0.03 $\displaystyle 0.03$

0.003 $\displaystyle 0.003$

$\sqrt{0.0009}$ $\displaystyle \sqrt{0.0009}$ is an undefined quantity.

0.0003 $\displaystyle 0.0003$

Correct answer:

0.03 $\displaystyle 0.03$

Explanation:

$0.0009= \frac{9}{10,000}$ $\displaystyle 0.0009= \frac{9}{10,000}$, so

$\sqrt{0.0009} = \sqrt{\frac{9}{10,000}}$ $\displaystyle \sqrt{0.0009} = \sqrt{\frac{9}{10,000}}$.

The square root of a fraction can be determined by taking the square roots of both numerator and denominator. Since $3^{2} = 9$ $\displaystyle 3^{2} = 9$, $\sqrt{9 } = 3$ $\displaystyle \sqrt{9 } = 3$, and since $100^{2} = 10,000$ $\displaystyle 100^{2} = 10,000$, $\sqrt{10,000} = 100$ $\displaystyle \sqrt{10,000} = 100$. Therefore,

$\sqrt{0.0009} = \sqrt{\frac{9}{10,000}} = \frac{\sqrt{9}}{\sqrt{10,000}} = \frac{3}{100} = 0.03$ $\displaystyle \sqrt{0.0009} = \sqrt{\frac{9}{10,000}} = \frac{\sqrt{9}}{\sqrt{10,000}} = \frac{3}{100} = 0.03$.

Report an Error

Example Question #14 : How To Find The Square Root

Note: The square root of a number is the number times itself. For example the square root of 4 is 2 because 2 x 2 = 4 or 2 squared is 4.

Find the square root of

$\sqrt{144}$ $\displaystyle \sqrt{144}$.

Possible Answers:

$\displaystyle 10$

$\displaystyle 12$

$\displaystyle 14$

$4^{2} \times 3^{2}$ $\displaystyle 4^{2} \times 3^{2}$

$12^{2}$ $\displaystyle 12^{2}$

Correct answer:

$\displaystyle 12$

Explanation:

So we are looking for a number that when it is squared is equal to 144. At this point you have to take some guesses.

$10^{2}=100$ $\displaystyle 10^{2}=100$

$11^{2}=121$ $\displaystyle 11^{2}=121$

Your getting closer

$13^{2}=169$ $\displaystyle 13^{2}=169$

So it must be between 11 and 13, lets try 12.

$12^{2}=144$ $\displaystyle 12^{2}=144$

So 12 is the answer.

Report an Error

View SSAT- Middle Level Tutors

Claire
Certified Tutor

Augustana College, Bachelor of Fine Arts, Music Teacher Education.

View SSAT- Middle Level Tutors

Errin
Certified Tutor

Converse College, Current Undergrad Student, Business Administration and Management.

View SSAT- Middle Level Tutors

Brianna
Certified Tutor

Fairfield University, Bachelor of Science, Biology, General. National University of Ireland at Galway, Master of Science, Neu...

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Chicago, Chemistry Tutors in San Francisco-Bay Area, Algebra Tutors in Seattle, French Tutors in Houston, ACT Tutors in Washington DC, Spanish Tutors in San Francisco-Bay Area, LSAT Tutors in New York City, French Tutors in Chicago, Computer Science Tutors in Phoenix, SAT Tutors in Philadelphia

Popular Courses & Classes

GRE Courses & Classes in Seattle, SSAT Courses & Classes in Phoenix, LSAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Denver, GMAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Denver, SAT Courses & Classes in Houston, SSAT Courses & Classes in Los Angeles, Spanish Courses & Classes in New York City, SSAT Courses & Classes in New York City

Popular Test Prep

SSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Denver, MCAT Test Prep in Denver, GMAT Test Prep in Los Angeles, ACT Test Prep in Houston, LSAT Test Prep in New York City, MCAT Test Prep in Philadelphia, GRE Test Prep in Seattle, SAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Squares / Square Roots

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #11 : Squares / Square Roots

Example Question #12 : Squares / Square Roots

Example Question #11 : Squares / Square Roots

Example Question #14 : Squares / Square Roots

Example Question #12 : Squares / Square Roots

Example Question #13 : How To Find The Square Root

Example Question #13 : Squares / Square Roots

Example Question #14 : Squares / Square Roots

Example Question #15 : Squares / Square Roots

Example Question #14 : How To Find The Square Root

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: