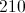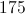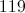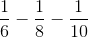All of the equations are given in slope-intercept form , so we can answer this question by examining the coefficients of , which are the slopes, and the constants, which are the -intercepts. In each case, since the lines are perpendicular, each -coefficient must be the other's opposite reciprocal, and since the lines have the same -intercept, the constants must be equal.

Of the five pairs, only 

 and 

and 

 and 

have equations whose -coefficients are the other's opposite reciprocal. Of these, only the latter pair of equations have equal constant terms. 

 and 

is the correct choice.

The slope of each line can be calculated by putting the equation in slope-intercept form  and noting the coefficient of :

Line 1:

Slope of Line 1: 

Line 2: 

Slope of Line 2: 

Line 3: The equation is already in slope-intercept form; its slope is 2.

Two lines are perpendicular if and only their slopes have product . The slopes of Lines 1 and 3 have product ; they are perpendicular. The slopes of Lines 1 and 2 have product ; they are not perpendicular. The slopes of Lines 2 and 3 have product ; they are not perpendicular. 

Correct response: Line 1 and Line 3 are perpendicular; Line 2 is perpendicular to neither.

Using the Pythagorean Theorem, the length of the second leg can be determined.

We are given the length of the hypotenuse and one leg.

The perimeter of the triangle is the sum of the lengths of the sides.

A right triangle with legs 6 feet and 8 feet has hypotentuse 10 feet, as this is a right triangle that confirms to the well-known Pythagorean triple 6-8-10. The perimeter is therefore  feet, or 8 yards.

We are looking for a polygon with this perimeter. Each choice is a polygon with all sides one yard long, so we want the polygon with eight sides - the regular octagon is the correct choice.

First, we need to use the Pythagorean Theorem to find the hypotenuse of the triangle.

Now, add up all three side lengths to find the perimeter of the triangle.

First, use the Pythagorean Theorem to find the length of the hypotenuse.

Substituting in  and  for  and  (the lengths of the triangle's legs), we get:

Now, add up the three sides to find the perimeter:

In order to find the perimeter  of the right triangle, we need to first find the missing length of the hypotenuse. In order to find the hypotenuse, use the Pythagorean Theorem:

, where  and  are the lengths of the legs of the triangle, and  is the length of the hypotenuse.

Substituting in our known values:

Now that we have the lengths of all sides of the right triangle, we can calculate the perimeter:

In order to find the perimeter  of the right triangle, we need to first find the missing length of the second leg. In order to find the second leg, use the Pythagorean Theorem:

, where  and  are the lengths of the legs of the triangle, and  is the length of the hypotenuse.

Substituting in our known values:

Subtracting  from each side of the equation lets us isolate the variable for which we are solving:

Now that we have the lengths of all three sides of the right triangle, we can calculate the perimeter :

In order to find the perimeter  of the right triangle, we need to first find the missing length of the hypotenuse. In order to find the length of the hypotenuse, use the Pythagorean Theorem:

, where  and  are the lengths of the legs of the triangle, and  is the length of the hypotenuse.

Substituting in our known values:

Now that we have all three sides of the right triangle, we can calculate the perimeter:

For the triangles to be similar, the dimensions of all sides must have the same ratio by dividing the 3-4-5 triangle.

The 6-8-10 triangle will have a scale factor of 2 since all dimensions are doubled the original 3-4-5 triangle.

The only correct answer that will yield similar ratios is the   triangle with a scale factor of 4 from the 3-4-5 triangle.  

The other answers will yield different ratios.