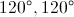Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #491 : Geometry

What is the area of a right triangle whose hypotenuse is 13 inches and whose legs each measure a number of inches equal to an integer?

Possible Answers:

$30 \;in^{2}$

$28 \;in^{2}$

It cannot be determined from the information given.

$25 \;in^{2}$

$32.5 \;in^{2}$

Correct answer:

$30 \;in^{2}$

Explanation:

We are looking for a Pythagorean triple - that is, three integers that satisfy the relationship $a^{2}+b^{2} = c^{2}$ . We know that c=13 , and the only Pythagorean triple with c=13 is (5,12,13) . The legs of the triangle are therefore 5 and 12, and the area of the right triangle is

$A = \frac{1}{2} bh= \frac{1}{2} \cdot 5\cdot 12 = 30$

Report an Error

Example Question #1 : How To Find If Right Triangles Are Congruent

Given:

$\bigtriangleup ABC$ , where $\angle B$ is a right angle; AB = 10; BC = 24 ;

$\bigtriangleup DEF$ , where $\angle E$ is a right angle and DF = 28 ;

$\bigtriangleup GHI$ , where $\angle H$ is a right angle and $\bigtriangleup GHI$ has perimeter 60;

$\bigtriangleup JKL$ , where $\angle K$ is a right angle and $\bigtriangleup JKL$ has area 120;

$\bigtriangleup MNO$ , where $\angle N$ is a right triangle and $\angle M \cong \angle A$

Which of the following must be a false statement?

Possible Answers:

$\bigtriangleup JKL \cong \bigtriangleup ABC$

All of the statements given in the other responses are possible

$\bigtriangleup DEF \cong \bigtriangleup ABC$

$\bigtriangleup GHI \cong \bigtriangleup ABC$

$\bigtriangleup MNO \cong \bigtriangleup ABC$

Correct answer:

$\bigtriangleup DEF \cong \bigtriangleup ABC$

Explanation:

$\bigtriangleup ABC$ has as its leg lengths 10 and 24, so the length of its hypotenuse, $\overline{AC}$ , is

$AC = \sqrt{(AB)^{2}+(BC)^{2}} = \sqrt{10^{2}+24^{2}} = \sqrt{100+576} = \sqrt{676 } = 26$

Its perimeter is the sum of its sidelengths:

P= 10+24+26 = 60

Its area is half the product of the lengths of its legs:

$A = \frac{1}{2} \cdot 10 \cdot 24 = 120$

$\bigtriangleup GHI$ and $\bigtriangleup JKL$ have the same perimeter and area, respectively, as $\bigtriangleup ABC$ ; also, between $\bigtriangleup MNO$ and $\bigtriangleup ABC$ , corresponding angles are congruent. In the absence of other information, none of these three triangles can be eliminated as being congruent to $\bigtriangleup ABC$ .

However, DF = 28 and AC = 26 . Therefore, $\overline{AC} \ncong \overline{DF}$ . Since a pair of corresponding sides is noncongruent, it follows that $\bigtriangleup DEF \ncong \bigtriangleup ABC$ .

Report an Error

Example Question #2 : How To Find If Right Triangles Are Congruent

Given: $\bigtriangleup ABC$ and $\bigtriangleup DEF$ with right angles $\angle B$ and $\angle E$ ; $\angle A \cong \angle D$ .

Which of the following statements alone, along with this given information, would prove that $\bigtriangleup ABC \cong \bigtriangleup DEF$ ?

I) $\overline{AB } \cong \overline{DE}$

II) $\overline{BC }\cong \overline{EF}$

III) $\overline{AC } \cong \overline{DF}$

Possible Answers:

I or III only

III only

II or III only

Any of I, II, or III

I or II only

Correct answer:

Any of I, II, or III

Explanation:

$\angle A \cong \angle D$ ; $\angle B \cong \angle E$ since both are right angles.

Given that two pairs of corresponding angles are congruent and any one side of corresponding sides is congruent, it follows that the triangles are congruent. In the case of Statement I, the included sides are congruent, so by the Angle-Side-Angle Congruence Postulate, $\bigtriangleup ABC \cong \bigtriangleup DEF$ . In the case of the other two statements, a pair of nonincluded sides are congruent, so by the Angle-Angle-Side Congruence Theorem, $\bigtriangleup ABC \cong \bigtriangleup DEF$ . Therefore, the correct choice is I, II, or III.

Report an Error

Example Question #1 : How To Find If Right Triangles Are Congruent

$\bigtriangleup ABC \cong \bigtriangleup DEF$ , where $\angle B$ is a right angle, AC = 20 , and AB = BC .

Which of the following is true?

Possible Answers:

$m \angle F = 60^{\circ }$

None of the statements given in the other choices is true.

$\bigtriangleup DEF$ has area 100

$DE = 20\sqrt{2}$

$\bigtriangleup DEF$ has perimeter 40

Correct answer:

$\bigtriangleup DEF$ has area 100

Explanation:

$\bigtriangleup ABC \cong \bigtriangleup DEF$ , and corresponding parts of congruent triangles are congruent.

Since $\angle B$ is a right angle, so is $\angle E$ . DE = AB and EF= BC ; since AB = BC , it follows that DE = EF . $\bigtriangleup DEF$ is an isosceles right triangle; consequently, $m \angle A = m \angle C = 45^{\circ }$ .

$\bigtriangleup DEF$ is a 45-45-90 triangle with hypotenuse of length DF= AC = 20 . By the 45-45-90 Triangle Theorem, the length of each leg is equal to that of the hypotenuse divided by $\sqrt{2}$ ; therefore,

$DE=EF = \frac{DF}{\sqrt{2}} = \frac{20}{\sqrt{2}} =\frac{20 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{20 \sqrt{2}}{2} = 10 \sqrt{2}$

$DE = 20\sqrt{2}$ is eliminated as the correct choice.

Also, the perimeter of $\bigtriangleup DEF$ is

$P = DE+EF+DF = 10 \sqrt{2} + 10 \sqrt{2} + 20 = 20+ 20 \sqrt{2} \ne 40$ .

This eliminates the perimeter of $\bigtriangleup DEF$ being 40 as the correct choice.

Also, $m \angle F = 60^{\circ }$ is eliminated as the correct choice, since the triangle is 45-45-90.

The area of $\bigtriangleup DEF$ is half the product of the lengths of its legs:

$A = \frac{1}{2} \cdot DE \cdot EF$

$= \frac{1}{2} \cdot 10 \sqrt{2}\cdot 10 \sqrt{2}$

$= \frac{1}{2} \cdot 10\cdot 10 \cdot \sqrt{2} \cdot \sqrt{2}$

$= \frac{1}{2} \cdot 10\cdot 10 \cdot 2$

= 100

The correct choice is the statement that $\bigtriangleup DEF$ has area 100.

Report an Error

Example Question #491 : Geometry

One angle of a right triangle has measure $120^{\circ }$ . Give the measures of the other two angles.

Possible Answers:

This triangle cannot exist.

$30^{\circ }, 30^{\circ }$

$30^{\circ }, 90^{\circ }$

$120^{\circ }, 120^{\circ }$

$90^{\circ }, 120^{\circ }$

Correct answer:

This triangle cannot exist.

Explanation:

A right triangle must have one right angle and two acute angles; this means that no angle of a right triangle can be obtuse. But since $120^{\circ } > 90^{\circ }$ , it is obtuse. This makes it impossible for a right triangle to have a $120^{\circ }$ angle.

Report an Error

Example Question #492 : Geometry

One angle of a right triangle has measure $68^{\circ }$ . Give the measures of the other two angles.

Possible Answers:

$22^{\circ }, 90^{\circ }$

This triangle cannot exist.

$44^{\circ },68^{\circ }$

$52^{\circ }, 60^{\circ }$

$56^{\circ },56^{\circ }$

Correct answer:

$22^{\circ }, 90^{\circ }$

Explanation:

One of the angles of a right triangle is by definition a right, or $90^{\circ }$ , angle, so this is the measure of one of the missing angles. Since the measures of the angles of a triangle total $180^{\circ }$ , if we let the measure of the third angle be , then:

x + 68 + 90 = 180

x + 158 = 180

x + 158 - 158= 180 - 158

x = 22

The other two angles measure $22 ^{\circ }, 90^{\circ }$ .

Report an Error

Example Question #3 : How To Find An Angle In A Right Triangle

Find the degree measure of in the right triangle below.

Possible Answers:

$90^{\circ}$

$43^{\circ}$

$32^{\circ}$

$47^{\circ}$

Correct answer:

$43^{\circ}$

Explanation:

The total number of degrees in a triangle is 180 .

While $47^{\circ}$ is provided as the measure of one of the angles in the diagram, you are also told that the triangle is a right triangle, meaning that it must contain a $90^{\circ}$ angle as well. To find the value of , subtract the other two degree measures from 180 .

$x=180-90-47=43^{\circ}$

Report an Error

Example Question #4 : How To Find An Angle In A Right Triangle

Find the angle value of .

Possible Answers:

$47^{\circ}$

$90^{\circ}$

$43^{\circ}$

$53^{\circ}$

Correct answer:

$43^{\circ}$

Explanation:

All the angles in a triangle must add up to 180 degrees.

$90^{\circ}+47^{\circ}+v=180^{\circ}$

$137^{\circ}+v=180^{\circ}$

$137^{\circ}+v-137^{\circ}=180^{\circ}-137^{\circ}$

$v=43^{\circ}$

Report an Error

Example Question #5 : How To Find An Angle In A Right Triangle

Find the angle value of .

Possible Answers:

$48^{\circ}$

$68^{\circ}$

$38^{\circ}$

$58^{\circ}$

Correct answer:

$58^{\circ}$

Explanation:

All the angles in a triangle adds up to $180^{\circ}$ .

$90^{\circ}+32^{\circ}+w=180^{\circ}$

$122^{\circ}+w=180^{\circ}$

$122^{\circ}+w-122^{\circ}=180^{\circ}-122^{\circ}$

$w=58^{\circ}$

Report an Error

Example Question #6 : How To Find An Angle In A Right Triangle

Find the angle value of .

Possible Answers:

$36^{\circ}$

$66^{\circ}$

$46^{\circ}$

$56^{\circ}$

Correct answer:

$46^{\circ}$

Explanation:

All the angles in a triangle add up to 180 degrees.

$90^{\circ}+44^{\circ}+y=180^{\circ}$

$134^{\circ}+y=180^{\circ}$

$134^{\circ}+y-134^{\circ}=180^{\circ}-134^{\circ}$

$y=46^{\circ}$

Report an Error

View SSAT- Upper Level Tutors

Nathan
Certified Tutor

University of the West Indies, Bachelor of Laws, Prelaw Studies.

View SSAT- Upper Level Tutors

Beverly
Certified Tutor

Wesleyan University, Bachelors, Mathematics. The University of Texas at Arlington, Masters, Linguistics.

View SSAT- Upper Level Tutors

Meg, M.Ed.
Certified Tutor

The University of Tennessee, Bachelor of Science, Hospitality Administration and Management. Lincoln Memorial University, Mas...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Dallas Fort Worth, SSAT Tutors in Los Angeles, LSAT Tutors in Washington DC, Math Tutors in Seattle, SAT Tutors in Seattle, Computer Science Tutors in Denver, SAT Tutors in Dallas Fort Worth, SAT Tutors in Atlanta, Algebra Tutors in Boston, SSAT Tutors in Denver

Popular Courses & Classes

MCAT Courses & Classes in New York City, GMAT Courses & Classes in Phoenix, GMAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Washington DC, SSAT Courses & Classes in Phoenix, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Phoenix, SAT Courses & Classes in Seattle, MCAT Courses & Classes in San Diego, GMAT Courses & Classes in Los Angeles

Popular Test Prep

SAT Test Prep in Atlanta, MCAT Test Prep in Seattle, GMAT Test Prep in Dallas Fort Worth, SAT Test Prep in Denver, SAT Test Prep in Boston, MCAT Test Prep in San Diego, ACT Test Prep in Boston, SSAT Test Prep in San Diego, MCAT Test Prep in Atlanta, GMAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #491 : Geometry

Example Question #1 : How To Find If Right Triangles Are Congruent

Example Question #2 : How To Find If Right Triangles Are Congruent

Example Question #1 : How To Find If Right Triangles Are Congruent

Example Question #491 : Geometry

Example Question #492 : Geometry

Example Question #3 : How To Find An Angle In A Right Triangle

Example Question #4 : How To Find An Angle In A Right Triangle

Example Question #5 : How To Find An Angle In A Right Triangle

Example Question #6 : How To Find An Angle In A Right Triangle

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: