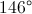All SSAT Upper Level Math Resources
Example Questions
Example Question #11 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #12 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #13 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #14 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #15 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #16 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #17 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #1 : Arithmetic Sequences
The angle measures of a pentagon form an arithmetic sequence. The smallest angle measures 
The measures of the five angles of a pentagon add up to 

If the measures of the five angles form an arithmetic sequence, the angles have measures increasing by a some common difference, 

Given this pattern and the total sum, we can solve for the common difference.
The greatest of the angle measures is given by 
Example Question #23 : Sequences And Series
Hunter makes 



The question is basically asking you to find the sum of the first 
To find the sum of a certain number of terms in an arithmetic sequence, use the following formula:
-
the number of the terms you have
-
the first term of the sequence
-
term of the sequence
To find the sum, we need to first find the 11th term of the sequence.
To find any term in an arithmetic sequence, use the following formula:
-
is the term we want to find
-
is the first term of the sequence
-
is the number of the term we want to find
-
is the common difference
Using the information given from the question,
Now, plug in the information to find the value of the 11th term.
Now that we know the 11th term of the sequence, we can plug in that value into the equation for the sum to find what these first 11 terms add up to.
Example Question #3 : How To Find The Answer To An Arithmetic Sequence
Find the 
To find any term in an arithmetic sequence, use the following formula:
-
is the term we want to find
-
is the first term of the sequence
-
is the number of the term we want to find
-
is the common difference
For this sequence,
Now, plug in the information to find the value of the 8th term.
Certified Tutor
Certified Tutor
All SSAT Upper Level Math Resources