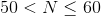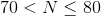All SSAT Upper Level Math Resources
Example Questions
Example Question #3 : Mixed / Improper Fractions
Which of the following is 80% of 
80% of a number is equal to 

Since 

Example Question #213 : Fractions
Which of the following is 
The correct answer is not among the other responses.
A number increased by 25% is 125%, or 


Example Question #5 : How To Find Out A Mixed Fraction From An Improper Fraction
Decrease 
Decreasing a number by 12.5% is the same as taking 87.5% of a number, or multiplying it by


Example Question #4 : Algebraic Fractions
Change to a mixed number
To convert from a fraction to a mixed number we must find out how many times the denominator goes into the numerator using division and the remainder becomes the new fraction.

Example Question #1341 : Ssat Upper Level Quantitative (Math)
Write 
Divide the numerator by the denominator.
Now, the whole number part will be 
Example Question #1342 : Ssat Upper Level Quantitative (Math)
If 
The numerator of the improper form of a mixed fraction is the original numerator added to the product of the integer and the original denominator:
Example Question #215 : Fractions
Rewrite 





The numerator of the improper form of a mixed fraction is the original numerator added to the product of the integer and the original denominator. The new denominator is the same as the old one. Therefore,

Add the numerator and the denominator: 
The correct response is 
Example Question #216 : Fractions
Rewrite 





The numerator of the improper form of a mixed fraction is the original numerator added to the product of the integer and the original denominator:
The correct response is 
Example Question #2 : How To Find Out An Improper Fraction From A Mixed Fraction
Rewrite 
The numerator of the improper form of a mixed fraction is the original numerator added to the product of the integer and the original denominator. The new denominator is the same as the old one. Therefore,
Add the numerator and the denominator:
Example Question #281 : Number Concepts And Operations
Change the following mixed number into an improper fraction in simplest form:
To change a mixed fraction into an improper fraction, keep the denominator the same.
To find the numerator, multiply the whole number part of the mixed fraction by the denominator, then add that value to the numerator.
Certified Tutor
Certified Tutor
All SSAT Upper Level Math Resources