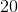All TACHS Math Resources
Example Questions
Example Question #22 : Math
Find the perimeter of a square with the following side length:
Possible Answers:
Correct answer:
Explanation:
Perimeters can be calculated by adding together the side lengths of a polygon. A square has four sides that are all the same length, therefore, we can write the following formula to solve for the perimeter.
We can rewrite this equation as the following:
In these equations the variable, 
Substitute the known side length and solve.
Example Question #1 : Circumference Of Circles
Find the circumference of a circle with the following radius:
Possible Answers:
Correct answer:
Explanation:
In order to find the circumference of a circle we will use the following formula:
In this equation, the variable, 
Substitute in for the circle's radius.
Simplify and solve.
All TACHS Math Resources
Popular Subjects
ACT Tutors in Chicago, Biology Tutors in San Diego, Math Tutors in Denver, Math Tutors in Phoenix, SSAT Tutors in Boston, Chemistry Tutors in Phoenix, Spanish Tutors in Seattle, ACT Tutors in Atlanta, MCAT Tutors in Phoenix, Statistics Tutors in Washington DC
Popular Courses & Classes
MCAT Courses & Classes in Boston, GMAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Atlanta, GRE Courses & Classes in Los Angeles, GRE Courses & Classes in San Diego, Spanish Courses & Classes in Denver, GRE Courses & Classes in Miami, GRE Courses & Classes in Denver, MCAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Los Angeles
Popular Test Prep
LSAT Test Prep in Chicago, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Washington DC, SSAT Test Prep in Miami, MCAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Atlanta, LSAT Test Prep in Atlanta, ISEE Test Prep in Seattle, SSAT Test Prep in Atlanta, GMAT Test Prep in Denver