Call Now to Set Up Tutoring:

(888) 888-0446

TACHS Math : Probability

Study concepts, example questions & explanations for TACHS Math

Create An Account

All TACHS Math Resources

43 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Probability Of Compound Events

When rolling a fair six-sided die and flipping a fair coin, what is the probability of rolling either a $\displaystyle 1$ or a $\displaystyle 6$ and getting heads on the coin flip?

Possible Answers:

$\frac{5}{6}$ $\displaystyle \frac{5}{6}$

$\frac{1}{6}$ $\displaystyle \frac{1}{6}$

$\frac{1}{4}$ $\displaystyle \frac{1}{4}$

$\frac{1}{8}$ $\displaystyle \frac{1}{8}$

Correct answer:

$\frac{1}{6}$ $\displaystyle \frac{1}{6}$

Explanation:

Recall what a probability is:

$\text{Probability}=\frac{\text{Number of desired outcomes}}{\text{Total number of outcomes}}$ $\displaystyle \text{Probability}=\frac{\text{Number of desired outcomes}}{\text{Total number of outcomes}}$

Start by finding the probability of rolling either $\displaystyle 1$ or $\displaystyle 6$ on a die. Since there are a total of $\displaystyle 6$ different outcomes, and we only want these two, the probability must be $\frac{2}{6}\text{, or }\frac{1}{3}$ $\displaystyle \frac{2}{6}\text{, or }\frac{1}{3}$ .

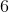
Next, find the probability of getting heads on a coin flip. Since we only want heads and there are only $\displaystyle 2$ possible outcomes on a coin flip, the probability of getting heads is $\frac{1}{2}$ $\displaystyle \frac{1}{2}$ .

Since the question wants the probability of both events occurring, you must multiply the probabilities together.

$\text{Probability of rolling 1 or 6 AND probability of flipping heads}=\frac{1}{3}\times \frac{1}{2}=\frac{1}{6}$ $\displaystyle \text{Probability of rolling 1 or 6 AND probability of flipping heads}=\frac{1}{3}\times \frac{1}{2}=\frac{1}{6}$

Report an Error

Example Question #1 : Probability Of Simple Events

What is the probability of rolling a one on a fair die?

Possible Answers:

$22\%$ $\displaystyle 22\%$

$16.\bar{6}\%$ $\displaystyle 16.\bar{6}\%$

$6\%$ $\displaystyle 6\%$

$18\%$ $\displaystyle 18\%$

Cannot be determined

Correct answer:

$16.\bar{6}\%$ $\displaystyle 16.\bar{6}\%$

Explanation:

In order to solve this problem, we need to discuss probabilities. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

$P=\frac{\textup{event: particular phenomenon we wish to observe}}{\textup{sample space: total number of possible outcomes}}$ $\displaystyle P=\frac{\textup{event: particular phenomenon we wish to observe}}{\textup{sample space: total number of possible outcomes}}$

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

$P=\frac{1}{6}$ $\displaystyle P=\frac{1}{6}$

Now, let's convert this into a percentage:

$\frac{1}{6}=0.1666$ $\displaystyle \frac{1}{6}=0.1666$

$0.1666\times100\%=16.\bar{6}\%$ $\displaystyle 0.1666\times100\%=16.\bar{6}\%$

Report an Error

View Tutors

Elena
Certified Tutor

University of Michigan-Dearborn, Bachelor of Science, Biological and Physical Sciences.

View Tutors

Darlene
Certified Tutor

Nicholls State University, Bachelor in Arts, Language Arts Teacher Education.

View Tutors

Allison
Certified Tutor

Asbury University, Bachelor of Education, Mathematics Teacher Education.

All TACHS Math Resources

43 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Seattle, ISEE Tutors in Denver, GRE Tutors in Miami, SAT Tutors in Boston, Calculus Tutors in Houston, Biology Tutors in San Diego, LSAT Tutors in Seattle, MCAT Tutors in Washington DC, Math Tutors in San Diego, LSAT Tutors in Washington DC

Popular Courses & Classes

GMAT Courses & Classes in Houston, SAT Courses & Classes in Phoenix, ISEE Courses & Classes in Miami, SAT Courses & Classes in San Diego, GMAT Courses & Classes in Atlanta, SSAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Washington DC, ISEE Courses & Classes in Seattle, GMAT Courses & Classes in Chicago, MCAT Courses & Classes in Phoenix

Popular Test Prep

GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in Atlanta, GMAT Test Prep in Denver, MCAT Test Prep in Washington DC, ISEE Test Prep in Los Angeles, MCAT Test Prep in Boston, GRE Test Prep in Miami, ISEE Test Prep in Washington DC, ACT Test Prep in Miami, GRE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

TACHS Math : Probability

Study concepts, example questions & explanations for TACHS Math

All TACHS Math Resources

Example Questions

Example Question #1 : Probability Of Compound Events

Example Question #1 : Probability Of Simple Events

All TACHS Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: