If Tim can ride his bike eight miles in one hour then we can write the following ratio:

\(\displaystyle \frac{8\textup{ miles}}{1\textup{ hour}}\)

Next, we want to know how long it will take him to ride forty miles. We can write the following ratio:

\(\displaystyle \frac{40\textup{ miles}}{x\textup{ hours}}\)

Next, we can set these equal to one another and form a proportion.

\(\displaystyle \frac{8\textup{ miles}}{1\textup{ hour}}=\frac{40\textup{ miles}}{x\textup{ hours}}\)

Cross multiply and solve for the variable.

\(\displaystyle \frac{8\textup{ miles}}{1\textup{ hour}}\times\frac{40\textup{ miles}}{x\textup{ hours}}\)

Simplify.

\(\displaystyle 8\times x=40\times1\)

\(\displaystyle 8x=40\)

Divide each side of the equation by \(\displaystyle 8\).

\(\displaystyle \frac{8x}{8}=\frac{40}{8}\)

Solve.

\(\displaystyle x=5\textup{ hours}\)

Let \(\displaystyle C\) be the cost of the pizza. Barry paid half the cost of the pizza, which is \(\displaystyle \frac{1}{2}C\); Jerry paid one third of the cost, which is \(\displaystyle \frac{1}{3}C\), and Mary paid $3. The sum of their shares of the cost is equal to the total cost, so the equation to set up is

\(\displaystyle C =\frac{1}{2}C+ \frac{1}{3}C + 3\)

Solve for \(\displaystyle C\) by isolating the variable at left. First, at right, collect the like terms by adding the coefficients of \(\displaystyle C\). This requires finding the least common denominator of the two fractions, which is 6:

\(\displaystyle C =\frac{1 \cdot 3}{2 \cdot 3}C+ \frac{1 \cdot 2}{3 \cdot 2}C + 3\)

\(\displaystyle C =\frac{ 3}{6}C+ \frac{2}{6}C + 3\)

\(\displaystyle C =\left (\frac{ 3}{6} + \frac{2}{6} \right )C + 3\)

\(\displaystyle C = \frac{5}{6} C + 3\)

Subtract \(\displaystyle \frac{5}{6} C\) from both sides, again by collecting like terms:

\(\displaystyle C - \frac{5}{6}C = \frac{5}{6} C + 3 - \frac{5}{6}C\)

\(\displaystyle \frac{6}{6} C - \frac{5}{6}C = 3\)

\(\displaystyle \left (\frac{6}{6} - \frac{5}{6} \right )C = 3\)

\(\displaystyle \frac{1}{6} C = 3\)

Now multiply both sides by 6 to reverse multiplication by \(\displaystyle \frac{1}{6}\):

\(\displaystyle 6\cdot \frac{1}{6} C =6 \cdot 3\)

\(\displaystyle C = 18\)

The pizza cost $18.

The average speed during a trip of \(\displaystyle d\) miles over a period of \(\displaystyle t\) hours is \(\displaystyle \frac{d}{t}\) miles per hour. Here, the distance driven is 40 miles; the time it took was two hours and fifteen minutes total minus the hour for the first 40 miles, which is one hour and fifteen minutes. Since fifteen minutes is equal to

\(\displaystyle \frac{15 \div 15 }{60 \div 15} = \frac{1}{4}\) hours, we get

\(\displaystyle d= 40\) and \(\displaystyle t = 1\frac{1}{4}\)

Therefore, the average speed traveled during the second part of the trip is

\(\displaystyle \frac{40}{1\frac{1}{4}}\)

\(\displaystyle = 40 \div 1\frac{1}{4}\)

\(\displaystyle = 40 \div \frac{5}{4}\)

\(\displaystyle = \frac{40}{1} \times \frac{4}{5}\)

\(\displaystyle = \frac{8}{1} \times \frac{4}{1}\)

\(\displaystyle = 32\) miles per hour.

Start by finding how many pieces of candy Maggie has. Since she has half as many as Jeremy, she must have \(\displaystyle 6\) pieces. Then, Jeremy and Maggie have \(\displaystyle 18\) pieces of candy together. Since Harold has twice as many as the two of them together, Harold must have \(\displaystyle 36\) pieces of candy.

Start by multiplying Taylor's age by \(\displaystyle 3\) to find her father's age.

\(\displaystyle 15\times 3 =45\)

Her father must be \(\displaystyle 45\) years old. Since her mother is two years older than her father, her mother must be \(\displaystyle 47\) years old.

Now, add up all their ages to find the sum of their ages.

\(\displaystyle 15+45+47=107\)

Start by finding how much weight Steve lost after the first month. Since he lost \(\displaystyle \frac{1}{12}\) of his starting weight of \(\displaystyle 240\), he must have lost \(\displaystyle 20\) pounds.

This means that at the end of his first month, he weighed \(\displaystyle 220\) pounds.

Since he lost \(\displaystyle 10\%\) of his remaining weight in the second month, he must have lost \(\displaystyle 22\) pounds from his \(\displaystyle 220\) pounds.

Thus, Steve must weigh \(\displaystyle 198\) pounds now.

Start by finding out how many books the \(\displaystyle 20\) full shelves can hold by multiplying it by the number of books held per shelf.

\(\displaystyle 20\times 325=6500\)

Next, find out how many books are held by the shelf that is not completely full.

\(\displaystyle 325 \times 0.8=260\)

Now, add the two together to find how many books total are in the library.

\(\displaystyle 6500+260=6760\)

In order to estimate the number of students in class, you will need to round the average number of students in a class up to \(\displaystyle 30\) and round the number of classes being held down to \(\displaystyle 30\) also.

Thus, \(\displaystyle 30 \times 30\) is easily doable in your head.

\(\displaystyle 30 \times 30 =900\)

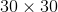
There are an estimated \(\displaystyle 900\) students in class at any given time.