All Trigonometry Resources
Example Questions
Example Question #1 : Trigonometry
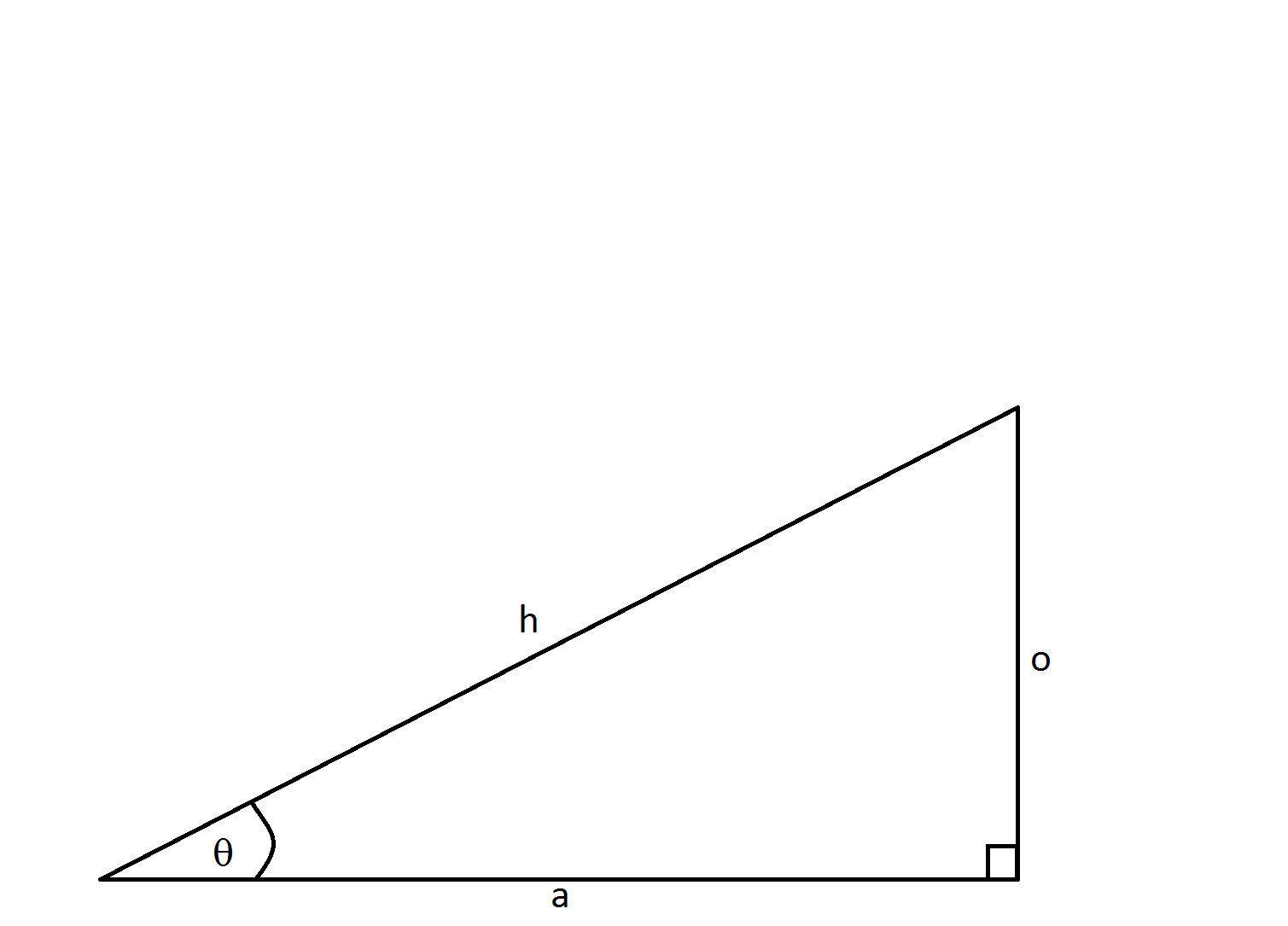
What is 


In order to find 



Now to find the measure of the angle using the 
If you calculated the angle's measure to be 
Example Question #21 : Trigonometric Operations

For the above triangle, what is 


We need to use a trigonometric function to find 


Example Question #22 : Trigonometric Operations

For the above triangle, what is 


We need to use a trigonometric function to find 


Example Question #23 : Trigonometric Operations
Which of the following is the degree equivalent of the inverse trigonometric function

The 


Therefore,
Example Question #24 : Trigonometric Operations
Assuming the angle in degrees, determine the value of 
To evaluate 
Inverse sine:
Inverse cosine:
Inverse tangent:
Evaluate each term. The final answers must return an angle.
Example Question #25 : Trigonometric Operations
If

what value(s) does 
Assume that 
No real solution.
If 
Since cosine and cosine inverse undo each other; we can then apply sine and secant inverse functions to obtain the solution.


are the two solutions.
Example Question #1 : Arcsin, Arccos, Arctan
Calculate 

The arcsecant function takes a trigonometric ratio on the unit circle as its input and results in an angle measure as its output. The given function can therefore be rewritten as

and is the angle measure 









Example Question #2 : Arcsin, Arccos, Arctan
Calculate 
The domain on the argument 


The range of the function 







Since 


or
for some x between 

Now, 


Therefore,

Certified Tutor
All Trigonometry Resources








































![D: [-1,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376547/gif.latex)
![R \textup{ (in radians)}: [-\frac{\pi}{2},\frac{\pi}{2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376557/gif.latex)
![D: [-1,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376549/gif.latex)
![R\textup{ (in radians)}: [0,\pi]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376558/gif.latex)



























