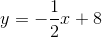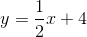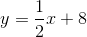Coordinate points are given x-coordinate first, y-coordinate second.  Quadrants are numbered counter-clockwise, with Quadrant I consisting of positive x-coordinates and positive y-coordinates, Quadrant II consisting of negative x-coordinates and positive y-coordinates, Quadrant III consisting of negative x-coordinates and negative y-coordinates, and Quadrant IV consisting of positive x-coordinates and negative y-coordinates.

(3, -2), Quadrant IV is correct because it lists the coordinates in the correct order and correctly identifies the Quadrant.

(3, -2), Quadrant II is incorrect because, while it lists the coordinates in the correct order, it misidentifies the Quadrant.

(-2, 3), Quadrant IV is incorrect because, while it correctly identifies the Quadrant, it lists the coordinates in the incorrect order.

(-2, 3), Quadrant II is incorrect because it both lists the coordinates in the incorrect order and misidentifies the Quadrant.

Coordinate points are given x-coordinate first, y-coordinate second.  The correct representation plots the point one unit to the left of the origin on the x-axis and four units up from the origin on the y-axis.

Coordinate points are given x-coordinate first, y-coordinate second.

(-2, 1), (2, 4) is correct because it list the coordinates of each point in the correct order.

(1, -2), (4, 2) is incorrect because it lists the coordinates of each point in the incorrect order.

(2, 4), (-2, 1) is incorrect because, while it lists the coordinates of each point correctly, it misidentifies the points.

(4, 2), (1, -2) is incorrect because it both lists the coordinates of each point in the incorrect order and misidentifies the points.

The distance formula is given by d = square root [(x₂ – x₁)² + (y₂ – y₁)²].  Let point 2 be (7,13) and point 1 be (1,5).  Substitute the values and solve.

The slope is found using the formula .

We know that the line contains the points (3,0) and (0,6). Using these points in the above equation allows us to calculate the slope.

The amplitude is half the measure from a trough to a peak.

The x-coordinate for the midpoint is given by taking the arithmetic average (mean) of the x-coordinates of the two end points. So the x-coordinate of the midpoint is given by 

The same procedure is used for the y-coordinates. So the y-coordinate of the midpoint is given by 

Thus the midpoint is given by the ordered pair 

 is the -intercept and equals .  can be solved for by substituting  in the equation for , which yields 

Plug in  for  to find a point on the line:

Thus,  is a point on the line.

Plug in   for  to find a second point on the line:

 is another point on the line.

Now we know that the line passes through the points  and .  

A quick sketch of the two points reveals that the line passes through all but the third quadrant.

First, we need to find the slope of the above line. 

The slope of a line. given two points  can be calculated using the slope formula

Set :

The slope of a line perpendicular to it has as its slope the opposite of the reciprocal of 2, which would be . Since we want this line to have the same -intercept as the first line, which is the point , we can substitute  and  in the slope-intercept form: