All AP Calculus AB Resources
Example Questions
Example Question #1211 : Ap Calculus Ab
Find the derivative of the following function:
Use 

Then the function 

By the chain rule, 
We calculate each term using the power rule:
Plug in 
Example Question #291 : Computation Of The Derivative
Let 
Find the second derivative of 
The second derivative is just the derivative of the first derivative. So first we find the first derivative of 




Then to get the second derivative, we just derive this function again. So
Example Question #51 : Calculus I — Derivatives
Define 
What is 
Take the derivative 


Example Question #52 : Calculus I — Derivatives
Define 
What is 
Take the derivative 


Example Question #55 : Calculus I — Derivatives
Define 
What is 
Rewrite:
Take the derivative 


Example Question #54 : Calculus I — Derivatives
What is the second derivative of 
To get the second derivative, first we need to find the first derivative.
To do that, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
Remember that anything to the zero power is one.
Now we do the same process again, but using 
Notice that 
Anything to the zero power is one.
Example Question #55 : Calculus I — Derivatives
What is the second derivative of 
Undefined
To get the second derivative, first we need to find the first derivative.
To do that, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
We're going to treat 

That means this problem will look like this:
Notice that 
Remember, anything to the zero power is one.
Now to get the second derivative we repeat those steps, but instead of using 

Notice that 
Example Question #56 : Calculus I — Derivatives
What is the second derivative of 
To get the second derivative, first we need to find the first derivative.
To do that, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
We're going to treat 

Notice that 
Now we repeat the process using 
Just like before, we're going to treat 

Example Question #61 : Calculus I — Derivatives
If 

The question is asking us for the second derivative of the equation. First, we need to find the first derivative.
To do that, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat 

Notice that 
Now we do the exact same process but using 
As stated earlier, anything to the zero power is one.
Example Question #62 : Calculus I — Derivatives
What is the second derivative of 
Undefined
To find the second derivative, first we need to find the first derivative.
To do that, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat 

Notice that 
That leaves us with 
Simplify.
As stated earlier, anything to the zero power is one, leaving us with:
Now we can repeat the process using 

As pointed out before, anything times zero is zero, meaning that 
All AP Calculus AB Resources




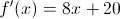























![g''(x) = - 2 \sin(x^2)-4x^2 \cos(x^2) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/65879/gif.latex)


![g''(x) = - 2 \cos(x^2)-4x^2 \sin(x^2) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/65882/gif.latex)

![g'(x) = 2x \cdot [-\sin (x^2)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/136830/gif.latex)

![g''(x) = - 2\left [ 1 \cdot \sin(x^2)+ x \cdot 2x \cos(x^2) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/109772/gif.latex)
![g''(x) = - 2\left [ \sin(x^2)+ 2x^2 \cos(x^2) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99997/gif.latex)
![g''(x) = - 2 \sin(x^2)-4x^2 \cos(x^2) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/136831/gif.latex)






&space;=&space;e%5E%7B-4x%7D)











)













































)






