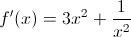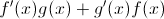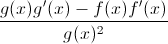To find the second derivative, first we need to find the first derivative.

To do that, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.

We're going to treat $\displaystyle 4$ as $\displaystyle 4x^0$ since anything to the zero power is one.

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{2-1})+(1*13x^{1-1})+(0*4x^{0-1})$

Notice that $\displaystyle (0*4x^{0-1})=0$ since anything times zero is zero.

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{2-1})+(1*13x^{1-1})$

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{1})+(1*13x^{0})$

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(24x^{1})+(13x^{0})$

Just like it was mentioned earlier, anything to the zero power is one.

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(24x)+(13*1)$

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=24x+13$

Now we repeat the process using $\displaystyle 24x+13$ as our expression.

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(1*24x^{1-1})+(0*13x^{0-1})$

Like before, anything times zero is zero.

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+10)=(1*24x^{1-1})$

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(24x^{0})$

Anything to the zero power is one.

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(24*1)$

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=24$

Take the derivative $\displaystyle g'$ of $\displaystyle g$, then take the derivative of $\displaystyle g'$.

$\displaystyle g(x) = 7x^{5} - 6x^{3} - 17x$

$\displaystyle g' (x) = 5\cdot 7x^{5-1} - 3\cdot 6x^{3-1} - 17$

$\displaystyle g' (x) = 35x^{4} - 18x^{2} - 17$

$\displaystyle g'' (x) = 4\cdot 35x^{4-1} - 2\cdot 18x^{2-1} - 0$

$\displaystyle g'' (x) = 140x^{3} - 36x$

To find the derivative at $\displaystyle x=2$, we first take the derivative of $\displaystyle f(x)$. By the derivative rule for logarithms,

$\displaystyle f'(x) = \frac{1}{x}$

Plugging in $\displaystyle x=2$, we get

$\displaystyle f'(2) = \frac{1}{2}$

Use the power rule on each term of the polynomial to get the derivative,

$\displaystyle f'(x) = (3)(4)x^2+1$

Now we plug in $\displaystyle x=3$

$\displaystyle f'(3) = (12)(3)^2 + 1 = 109$

We need to find the first derivative of f(x). This will require us to apply both the Product and Chain Rules. When we apply the Product Rule, we obtain:

$\displaystyle f'(x)=\sin(x^2)\cdot\frac{\mathrm{d} }{\mathrm{d} x}[x^2]+x^2\cdot\frac{\mathrm{d} }{\mathrm{d} x}[\sin(x^2)]$

In order to find the derivative of $\displaystyle \sin(x^2)$, we will need to employ the Chain Rule.

 $\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}[\sin(x^2)]=\cos(x^2)\cdot\frac{\mathrm{d} }{\mathrm{d} x}[x^2]=\cos(x^2)\cdot2x$

$\displaystyle f'(x)=\sin(x^2)\cdot2x + x^2\cdot\cos(x^2)\cdot2x$

 We can factor out a 2x to make this a little nicer to look at.

$\displaystyle f'(x)=2x(\sin(x^2)+x^2\cos(x^2))$

Now we must evaluate the derivative when x = $\displaystyle \frac{\sqrt{\pi}}{2}$.

$\displaystyle f'\left (\frac{\sqrt{\pi}}{2} \right )=2\cdot\frac{\sqrt{\pi}}{2}(\sin\frac{\pi}{4}+\frac{\pi}{4}\cos\frac{\pi}{4})$

$\displaystyle =\sqrt{\pi}(\frac{\sqrt{2}}{2}+\frac{\pi\sqrt{2}}{8})=\sqrt{2\pi}(\frac{1}{2}+\frac{\pi}{8})=\frac{\sqrt{2\pi}(\pi + 4)}{8}$

The answer is $\displaystyle \frac{\sqrt{2\pi}(\pi + 4)}{8}$.

Since this function is a polynomial, we take the derivative of each term separately.

From the power rule, the derivative of 

$\displaystyle x^3$

is simply

$\displaystyle 3x^2$

We can rewrite $\displaystyle \frac{1}{x}$ as

$\displaystyle x^{-1}$

and using the power rule again, we get a derivative of

$\displaystyle -x^{-2}$ or $\displaystyle -\frac{1}{x^2}$

So the answer is

$\displaystyle f'(x) = 3x^2-\frac{1}{x^2}$

The chain rule is "first times the derivative of the second plus second times derivative of the first".

In this case, that means $\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}f(x)*g(x)\mathrm{d x} =f(x)g'(x)+f'(x)g(x)$.

The question is just asking for the Quotient Rule formula.

Recall the Quotient Rule is the bottom function times the derivative of the top minus the top function times the derivative of the bottom all divided by the bottom function squared.

Given,

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\frac{f(x)}{g(x)}$

the bottom function is $\displaystyle g(x)$ and the top function is $\displaystyle f(x)$. This makes the bottom derivative $\displaystyle g'(x)$ and the top derivative $\displaystyle f'(x)$.

Substituting these into the Quotient Rule formula resulting in the following.

$\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\frac{f(x)}{g(x)}=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{(g(x))^2}$

The derivative must be computed using the product rule.  Because the derivative of $\displaystyle x^2$ brings a $\displaystyle 2$ down as a coefficient, it can be combined with $\displaystyle 2^x$ to give $\displaystyle 2^{x+1}$

$\displaystyle f(x) = 5 ^{x + 1} = 5 ^{1} \cdot 5 ^{x } = 5 \cdot 5 ^{x }$

Therefore, 

$\displaystyle f'(x) = 5 \cdot \frac{\mathrm{d} }{\mathrm{d} x} \left ( 5 ^{x } \right )$

$\displaystyle \frac{\mathrm{d}}{\mathrm{d} x} \left ( a ^{x } \right ) = \ln a \cdot a ^{x }$ for any real $\displaystyle a$, so $\displaystyle \frac{\mathrm{d} }{\mathrm{d} x} \left ( 5 ^{x } \right ) = \ln 5 \cdot 5 ^{x}$, and

$\displaystyle f'(x) = 5 \ln 5 \cdot 5 ^{x} = \ln 5 \cdot 5 \cdot 5 ^{x} = \ln 5 \cdot 5 ^{x+1}$