Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 4th Grade Math : Build fractions from unit fractions

Study concepts, example questions & explanations for Common Core: 4th Grade Math

Create An Account

All Common Core: 4th Grade Math Resources

7 Diagnostic Tests 189 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Subtracting Fractions In Word Problems

This year, Emily grew $\frac{1}{6}$ $\displaystyle \frac{1}{6}$ of an inch, and her brother, Dan, grew $\frac{4}{6}$ $\displaystyle \frac{4}{6}$ of an inch. How much more did Dan grow than Emily?

Possible Answers:

$\frac{5}{6}$ $\displaystyle \frac{5}{6}$

$\frac{3}{6}$ $\displaystyle \frac{3}{6}$

$\frac{4}{6}$ $\displaystyle \frac{4}{6}$

$\frac{2}{6}$ $\displaystyle \frac{2}{6}$

$\frac{1}{6}$ $\displaystyle \frac{1}{6}$

Correct answer:

$\frac{3}{6}$ $\displaystyle \frac{3}{6}$

Explanation:

The phrase, "how much more" tells as that we want to find the difference in how much they've grown.

$\frac{4}{6}-\frac{1}{6}=\frac{3}{6}$ $\displaystyle \frac{4}{6}-\frac{1}{6}=\frac{3}{6}$

Report an Error

Example Question #1229 : Common Core Math: Grade 4

This year, Cassie grew $\frac{3}{9}$ $\displaystyle \frac{3}{9}$ of an inch, and her brother, Charlie, grew $\frac{5}{9}$ $\displaystyle \frac{5}{9}$ of an inch. How much more did Charlie grow than Cassie?

Possible Answers:

$\frac{2}{9}$ $\displaystyle \frac{2}{9}$

$\frac{6}{9}$ $\displaystyle \frac{6}{9}$

$\frac{4}{9}$ $\displaystyle \frac{4}{9}$

$\frac{5}{9}$ $\displaystyle \frac{5}{9}$

$\frac{1}{9}$ $\displaystyle \frac{1}{9}$

Correct answer:

$\frac{2}{9}$ $\displaystyle \frac{2}{9}$

Explanation:

The phrase, "how much more" tells as that we want to find the difference in how much they've grown.

$\frac{5}{9}-\frac{3}{9}=\frac{2}{9}$ $\displaystyle \frac{5}{9}-\frac{3}{9}=\frac{2}{9}$

Report an Error

Example Question #602 : Number & Operations: Fractions

A baker used $\frac{1}{7}$ $\displaystyle \frac{1}{7}$ of a package of sprinkles and $\frac{6}{7}$ $\displaystyle \frac{6}{7}$ of a package of icing when decorating a cake. How much more icing than sprinkles did the baker use?

Possible Answers:

$\frac{5}{7}$ $\displaystyle \frac{5}{7}$

$\frac{2}{7}$ $\displaystyle \frac{2}{7}$

$\frac{3}{7}$ $\displaystyle \frac{3}{7}$

$\frac{4}{7}$ $\displaystyle \frac{4}{7}$

$\frac{6}{}7$ $\displaystyle \frac{6}{}7$

Correct answer:

$\frac{5}{7}$ $\displaystyle \frac{5}{7}$

Explanation:

The phrase, "how much more" tells as that we want to find the difference, so we subtract.

$\frac{6}{7}-\frac{1}{7}=\frac{5}{7}$ $\displaystyle \frac{6}{7}-\frac{1}{7}=\frac{5}{7}$

5 7

Report an Error

Example Question #1231 : Common Core Math: Grade 4

A baker used $\frac{3}{7}$ $\displaystyle \frac{3}{7}$ of a package of sprinkles and $\frac{6}{7}$ $\displaystyle \frac{6}{7}$ of a package of icing when decorating a cake. How much more icing than sprinkles did the baker use?

Possible Answers:

$\frac{3}{7}$ $\displaystyle \frac{3}{7}$

$\frac{1}{7}$ $\displaystyle \frac{1}{7}$

$\frac{2}{7}$ $\displaystyle \frac{2}{7}$

$\frac{4}{7}$ $\displaystyle \frac{4}{7}$

$\frac{5}{7}$ $\displaystyle \frac{5}{7}$

Correct answer:

$\frac{3}{7}$ $\displaystyle \frac{3}{7}$

Explanation:

The phrase, "how much more" tells as that we want to find the difference, so we subtract.

$\frac{6}{7}-\frac{3}{7}=\frac{3}{7}$ $\displaystyle \frac{6}{7}-\frac{3}{7}=\frac{3}{7}$

3 7

Report an Error

Example Question #1232 : Common Core Math: Grade 4

A baker used $\frac{3}{7}$ $\displaystyle \frac{3}{7}$ of a package of sprinkles and $\frac{5}{7}$ $\displaystyle \frac{5}{7}$ of a package of icing when decorating a cake. How much more icing than sprinkles did the baker use?

Possible Answers:

$\frac{1}{7}$ $\displaystyle \frac{1}{7}$

$\frac{5}{7}$ $\displaystyle \frac{5}{7}$

$\frac{3}{7}$ $\displaystyle \frac{3}{7}$

$\frac{2}{7}$ $\displaystyle \frac{2}{7}$

$\frac{4}{7}$ $\displaystyle \frac{4}{7}$

Correct answer:

$\frac{2}{7}$ $\displaystyle \frac{2}{7}$

Explanation:

The phrase, "how much more" tells as that we want to find the difference, so we subtract.

$\frac{5}{7}-\frac{3}{7}=\frac{2}{7}$ $\displaystyle \frac{5}{7}-\frac{3}{7}=\frac{2}{7}$

2 7

Report an Error

Example Question #1233 : Common Core Math: Grade 4

A baker used $\frac{2}{7}$ $\displaystyle \frac{2}{7}$ of a package of sprinkles and $\frac{3}{7}$ $\displaystyle \frac{3}{7}$ of a package of icing when decorating a cake. How much more icing than sprinkles did the baker use?

Possible Answers:

$\frac{5}{7}$ $\displaystyle \frac{5}{7}$

$\frac{4}{7}$ $\displaystyle \frac{4}{7}$

$\frac{1}{}7$ $\displaystyle \frac{1}{}7$

$\frac{2}{7}$ $\displaystyle \frac{2}{7}$

$\frac{3}{7}$ $\displaystyle \frac{3}{7}$

Correct answer:

$\frac{1}{}7$ $\displaystyle \frac{1}{}7$

Explanation:

The phrase, "how much more" tells as that we want to find the difference, so we subtract.

$\frac{3}{7}-\frac{2}{7}=\frac{1}{7}$ $\displaystyle \frac{3}{7}-\frac{2}{7}=\frac{1}{7}$

1 7

Report an Error

Example Question #71 : Solve Word Problems Involving Addition And Subtraction Of Fractions: Ccss.Math.Content.4.Nf.B.3d

A baker used $\frac{1}{3}$ $\displaystyle \frac{1}{3}$ of a package of sprinkles and $\frac{2}{3}$ $\displaystyle \frac{2}{3}$ of a package of icing when decorating a cake. How much more icing than sprinkles did the baker use?

Possible Answers:

$\frac{1}{3}$ $\displaystyle \frac{1}{3}$

$\frac{4}{3}$ $\displaystyle \frac{4}{3}$

$\frac{5}{3}$ $\displaystyle \frac{5}{3}$

$\frac{3}{3}$ $\displaystyle \frac{3}{3}$

$\frac{2}{3}$ $\displaystyle \frac{2}{3}$

Correct answer:

$\frac{1}{3}$ $\displaystyle \frac{1}{3}$

Explanation:

The phrase, "how much more" tells as that we want to find the difference, so we subtract.

$\frac{2}{3}-\frac{1}{3}=\frac{1}{3}$ $\displaystyle \frac{2}{3}-\frac{1}{3}=\frac{1}{3}$

1 3

Report an Error

Example Question #301 : Build Fractions From Unit Fractions

Select the fraction model that shows the sum of $\frac{1}{3}+\frac{1}{3}$ $\displaystyle \frac{1}{3}+\frac{1}{3}$

Possible Answers:

2 6

3 6

2 3

3 4

2 4

Correct answer:

2 3

Explanation:

$\frac{1}{3}+\frac{1}{3}=\frac{2}{3}$ $\displaystyle \frac{1}{3}+\frac{1}{3}=\frac{2}{3}$

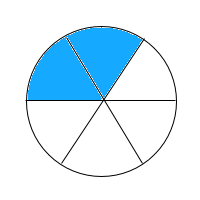
The fraction model is broken up into three pieces and two of the pieces are shaded in. The numerator of the fraction tells us how many pieces should be shaded in, and the denominator tells us how many pieces the whole should be split up into.

Report an Error

Example Question #302 : Build Fractions From Unit Fractions

Select the fraction model that shows the sum of $\frac{1}{4}+\frac{1}{4}$ $\displaystyle \frac{1}{4}+\frac{1}{4}$

Possible Answers:

3 6

2 3

3 4

2 4

2 6

Correct answer:

2 4

Explanation:

$\frac{1}{4}+\frac{1}{4}=\frac{2}{4}$ $\displaystyle \frac{1}{4}+\frac{1}{4}=\frac{2}{4}$

The fraction model is broken up into four pieces and two of the pieces are shaded in. The numerator of the fraction tells us how many pieces should be shaded in, and the denominator tells us how many pieces the whole should be split up into.

Report an Error

Example Question #3 : Understand Addition And Subtraction Of Fractions: Ccss.Math.Content.4.Nf.B.3a

Select the fraction model that shows the sum of $\frac{1}{4}+\frac{2}{4}$ $\displaystyle \frac{1}{4}+\frac{2}{4}$

Possible Answers:

3 4

2 4

2 6

3 6

2 3

Correct answer:

3 4

Explanation:

$\frac{1}{4}+\frac{2}{4}=\frac{3}{4}$ $\displaystyle \frac{1}{4}+\frac{2}{4}=\frac{3}{4}$

The fraction model is broken up into four pieces and three of the pieces are shaded in. The numerator of the fraction tells us how many pieces should be shaded in, and the denominator tells us how many pieces the whole should be split up into.

Report an Error

View Tutors

Jamie
Certified Tutor

East Central University, Bachelors, Special Education.

View Tutors

Patrick
Certified Tutor

Florida International University, Bachelors, Psychology. Florida International University, Masters, Psychology.

View Tutors

Marlene
Certified Tutor

Herbert Lehman, Bachelors, Recreation Education. Long Island University-Brooklyn Campus, Masters, Special Education.

All Common Core: 4th Grade Math Resources

7 Diagnostic Tests 189 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in San Francisco-Bay Area, GRE Tutors in Denver, English Tutors in Boston, SAT Tutors in Seattle, LSAT Tutors in Chicago, MCAT Tutors in Dallas Fort Worth, Math Tutors in Houston, Calculus Tutors in Philadelphia, Reading Tutors in Houston, SAT Tutors in Los Angeles

Popular Courses & Classes

SAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Houston, LSAT Courses & Classes in Houston, SAT Courses & Classes in New York City, GMAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Washington DC, SAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Los Angeles, GRE Courses & Classes in Denver, LSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SSAT Test Prep in Houston, GMAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Seattle, LSAT Test Prep in Los Angeles, GRE Test Prep in Atlanta, SAT Test Prep in Washington DC, LSAT Test Prep in Houston, GRE Test Prep in Denver, SSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 4th Grade Math : Build fractions from unit fractions

Study concepts, example questions & explanations for Common Core: 4th Grade Math

All Common Core: 4th Grade Math Resources

Example Questions

Example Question #31 : Subtracting Fractions In Word Problems

Example Question #1229 : Common Core Math: Grade 4

Example Question #602 : Number & Operations: Fractions

Example Question #1231 : Common Core Math: Grade 4

Example Question #1232 : Common Core Math: Grade 4

Example Question #1233 : Common Core Math: Grade 4

Example Question #71 : Solve Word Problems Involving Addition And Subtraction Of Fractions: Ccss.Math.Content.4.Nf.B.3d

Example Question #301 : Build Fractions From Unit Fractions

Example Question #302 : Build Fractions From Unit Fractions

Example Question #3 : Understand Addition And Subtraction Of Fractions: Ccss.Math.Content.4.Nf.B.3a

All Common Core: 4th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback:

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 4th Grade Math : Build fractions from unit fractions

Study concepts, example questions & explanations for Common Core: 4th Grade Math

All Common Core: 4th Grade Math Resources

Example Questions

Example Question #31 : Subtracting Fractions In Word Problems

Example Question #1229 : Common Core Math: Grade 4

Example Question #602 : Number & Operations: Fractions

Example Question #1231 : Common Core Math: Grade 4

Example Question #1232 : Common Core Math: Grade 4

Example Question #1233 : Common Core Math: Grade 4

Example Question #71 : Solve Word Problems Involving Addition And Subtraction Of Fractions: Ccss.Math.Content.4.Nf.B.3d

Example Question #301 : Build Fractions From Unit Fractions

Example Question #302 : Build Fractions From Unit Fractions

Example Question #3 : Understand Addition And Subtraction Of Fractions: Ccss.Math.Content.4.Nf.B.3a

All Common Core: 4th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Example Question #602 : Number & Operations: Fractions