Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 6th Grade Math : Fluently Divide Multi-Digit Numbers: CCSS.Math.Content.6.NS.B.2

Study concepts, example questions & explanations for Common Core: 6th Grade Math

Create An Account

All Common Core: 6th Grade Math Resources

6 Diagnostic Tests 186 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3452 : Operations

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 21\\ 9{\overline{\smash{)}189}}\\ -\ 18 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{9\ \ }\\ -\ \ \ 9\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$9\times 18$

$9\times 21$

$9\times 32$

$9\times 23$

$9\times 27$

Correct answer:

$9\times 21$

Explanation:

The computation shows that $189\div9=21$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 21}\\ {\color{Green} 9}{\overline{\smash{)}189}}\\ -\ 18 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 9\ \ }\\ -\ \ \ 9\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$9\times21=189+0$

Simplify.

$9\times21=189$

The correct answer is $9\times 21$

Report an Error

Example Question #3453 : Operations

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 31\\ 9{\overline{\smash{)}279}}\\ -\ 27 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{9\ \ }\\ -\ \ \ 9\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$9\times 36$

$3\times 93$

$9\times 33$

$9\times 31$

$9\times 93$

Correct answer:

$9\times 31$

Explanation:

The computation shows that $279\div9=31$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 31}\\ {\color{Green} 9}{\overline{\smash{)}279}}\\ -\ 27 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 9\ \ }\\ -\ \ \ 9\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$9\times31=279+0$

Simplify.

$9\times31=279$

The correct answer is $9\times 31$

Report an Error

Example Question #11 : Fluently Divide Multi Digit Numbers: Ccss.Math.Content.6.Ns.B.2

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 21\\ 7{\overline{\smash{)}147}}\\ -\ 14 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{7\ \ }\\ -\ \ \ 7\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$7\times 28$

$7\times 31$

$7\times 21$

$7\times 41$

$7\times 17$

Correct answer:

$7\times 21$

Explanation:

The computation shows that $147\div7=21$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 21}\\ {\color{Green} 7}{\overline{\smash{)}147}}\\ -\ 14 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 7\ \ }\\ -\ \ \ 7\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$7\times21=147+0$

Simplify.

$7\times21=147$

The correct answer is $7\times 21$

Report an Error

Example Question #551 : How To Divide

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 31\\ 7{\overline{\smash{)}217}}\\ -\ 21 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{7\ \ }\\ -\ \ \ 7\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$7\times 31$

$7\times 28$

$7\times 21$

$7\times 34$

$7\times 23$

Correct answer:

$7\times 31$

Explanation:

The computation shows that $217\div7=31$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 31}\\ {\color{Green} 7}{\overline{\smash{)}217}}\\ -\ 21 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 7\ \ }\\ -\ \ \ 7\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$7\times31=217+0$

Simplify.

$7\times31=217$

The correct answer is $7\times 31$

Report an Error

Example Question #3674 : Numbers And Operations

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 41\\ 7{\overline{\smash{)}287}}\\ -\ 28 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{7\ \ }\\ -\ \ \ 7\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$7\times 21$

$7\times 32$

$7\times 28$

$7\times 41$

$7\times 31$

Correct answer:

$7\times 41$

Explanation:

The computation shows that $287\div7=41$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 41}\\ {\color{Green} 7}{\overline{\smash{)}287}}\\ -\ 28 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 7\ \ }\\ -\ \ \ 7\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$7\times41=287+0$

Simplify.

$7\times41=287$

The correct answer is $7\times 41$

Report an Error

Example Question #3455 : Operations

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 31\\ 6{\overline{\smash{)}186}}\\ -\ 18 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{6\ \ }\\ -\ \ \ 6\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$6\times 27$

$6\times 41$

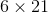
$6\times 21$

$6\times 31$

$6\times 36$

Correct answer:

$6\times 31$

Explanation:

The computation shows that $186\div6=31$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 31}\\ {\color{Green} 6}{\overline{\smash{)}186}}\\ -\ 18 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 6\ \ }\\ -\ \ \ 6\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$6\times31=186+0$

Simplify.

$6\times31=186$

The correct answer is $6\times 31$

Report an Error

Example Question #3456 : Operations

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 21\\ 8{\overline{\smash{)}168}}\\ -\ 16 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{8\ \ }\\ -\ \ \ 8\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$8\times 11$

$8\times 21$

$8\times 41$

$8\times 31$

$8\times 27$

Correct answer:

$8\times 21$

Explanation:

The computation shows that $168\div8=21$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 21}\\ {\color{Green} 8}{\overline{\smash{)}168}}\\ -\ 16 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 8\ \ }\\ -\ \ \ 8\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$8\times21=168+0$

Simplify.

$8\times21=168$

The correct answer is $8\times 21$

Report an Error

Example Question #3457 : Operations

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 31\\ 8{\overline{\smash{)}248}}\\ -\ 24 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{8\ \ }\\ -\ \ \ 8\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$8\times 27$

$8\times 21$

$8\times 31$

$8\times 41$

$8\times 32$

Correct answer:

$8\times 31$

Explanation:

The computation shows that $248\div8=31$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 31}\\ {\color{Green} 8}{\overline{\smash{)}248}}\\ -\ 24 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 8\ \ }\\ -\ \ \ 8\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$8\times31=248+0$

Simplify.

$8\times31=248$

The correct answer is $8\times 31$

Report an Error

Example Question #3458 : Operations

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 41\\ 8{\overline{\smash{)}328}}\\ -\ 32 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{8\ \ }\\ -\ \ \ 8\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$8\times 31$

$8\times 51$

$8\times 41$

$8\times 27$

$8\times 38$

Correct answer:

$8\times 41$

Explanation:

The computation shows that $328\div8=41$ with a remainder of .

$\frac{\begin{array}[b]{r} \ {\color{Green} 41}\\ {\color{Green} 8}{\overline{\smash{)}328}}\\ -\ 32 \smash{\downarrow}\end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{ 8\ \ }\\ -\ \ \ 8\ \ \end{array}}{ \ \ \ \space} }$

So it must be that:

$8\times41=328+0$

Simplify.

$8\times41=328$

The correct answer is $8\times 41$

Report an Error

Example Question #3461 : Operations

Use the computation shown to find the products:

$\frac{\begin{array}[b]{r} \ 31\\ 9{\overline{\smash{)}279}}\\ -\ 27 \ \smash \ \end{array}}{ \ \ \ \space \frac{\begin{array}[b]{r}00{9\ \ }\\ -\ \ \ 9\ \ \end{array}}{ \ \ \ \space} }$

Possible Answers:

$9\times 31$

$9\times 27$

$9\times 21$

$9\times 41$

$9\times 12$

Correct answer:

$9\times 31$

Explanation:

The computation shows that $279\div9=31$ with a remainder of .

So it must be that:

$9\times31=279+0$

Simplify.

$9\times31=279$

The correct answer is $9\times 31$

Report an Error

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

View Tutors

David
Certified Tutor

Kent State University, Bachelors, Marketing. Kent State University at Kent, Masters in Education, Special Education.

All Common Core: 6th Grade Math Resources

6 Diagnostic Tests 186 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in New York City, French Tutors in Denver, Statistics Tutors in Boston, Physics Tutors in Miami, Spanish Tutors in Miami, Reading Tutors in Dallas Fort Worth, GRE Tutors in San Diego, GMAT Tutors in Miami, Reading Tutors in San Francisco-Bay Area, Statistics Tutors in New York City

Popular Courses & Classes

SAT Courses & Classes in Boston, SAT Courses & Classes in Seattle, ACT Courses & Classes in San Diego, ISEE Courses & Classes in San Diego, Spanish Courses & Classes in Denver, ACT Courses & Classes in Atlanta, GMAT Courses & Classes in Washington DC, GRE Courses & Classes in Washington DC, ACT Courses & Classes in Philadelphia, ISEE Courses & Classes in Atlanta

Popular Test Prep

ISEE Test Prep in Washington DC, ACT Test Prep in Philadelphia, ISEE Test Prep in Atlanta, MCAT Test Prep in Boston, ACT Test Prep in Atlanta, SSAT Test Prep in New York City, ACT Test Prep in Washington DC, GMAT Test Prep in New York City, LSAT Test Prep in Chicago, SAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 6th Grade Math : Fluently Divide Multi-Digit Numbers: CCSS.Math.Content.6.NS.B.2

Study concepts, example questions & explanations for Common Core: 6th Grade Math

All Common Core: 6th Grade Math Resources

Example Questions

Example Question #3452 : Operations

Example Question #3453 : Operations

Example Question #11 : Fluently Divide Multi Digit Numbers: Ccss.Math.Content.6.Ns.B.2

Example Question #551 : How To Divide

Example Question #3674 : Numbers And Operations

Example Question #3455 : Operations

Example Question #3456 : Operations

Example Question #3457 : Operations

Example Question #3458 : Operations

Example Question #3461 : Operations

All Common Core: 6th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: