In order to find the eigenvalues of a matrix, apply the following formula:

\(\displaystyle det(A-\lambda I) =0\)

\(\displaystyle I\) is the identity matrix.

\(\displaystyle \begin{bmatrix} 1&2 \\ -2&1 \end{bmatrix}-\lambda \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix}=\begin{bmatrix} 1-\lambda & 2\\ -2&1-\lambda \end{bmatrix}\)

Compute the determinant and set it equal to zero.

\(\displaystyle (1-\lambda)(1-\lambda)-(2)(-2)=0\)

\(\displaystyle 1-2\lambda+\lambda^2+4=0\)

\(\displaystyle \lambda^2-2\lambda+5=0\)

Solve for lambda by using the quadratic formula.

\(\displaystyle \lambda_{1,2}=1\pm2i\)

In order to find the eigenvalues of a matrix, apply the following formula:

\(\displaystyle det(A-\lambda I) =0\)

\(\displaystyle I\) is the identity matrix.

\(\displaystyle \begin{bmatrix} 1&2 \\ -2&1 \end{bmatrix}-\lambda \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix}=\begin{bmatrix} 1-\lambda & 2\\ -2&1-\lambda \end{bmatrix}\)

Compute the determinant and set it equal to zero.

\(\displaystyle (1-\lambda)(1-\lambda)-(2)(-2)=0\)

\(\displaystyle 1-2\lambda+\lambda^2+4=0\)

\(\displaystyle \lambda^2-2\lambda+5=0\)

Solve for lambda by using the quadratic formula.

\(\displaystyle \lambda_{1,2}=1\pm2i\)

The fifth degree Taylor polynomial approximating \(\displaystyle sin(x)\) centered at \(\displaystyle x=0\) is: 

\(\displaystyle sin(x) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!}\)

The Lagrange error is the absolute value of the next term in the sequence, which is equal to \(\displaystyle \left |\frac{x^7}{7!} \right |\).

We need only evaluate this at \(\displaystyle x=1\) and thus we obtain \(\displaystyle \frac{1^7}{7!} = \frac{1}{7!}\)

We can show that the series \(\displaystyle \sum_{i=0}^{\infty} \frac{n!}{n^2 cos(n)}\)  diverges using the ratio test.

\(\displaystyle L = \lim_{n ->\infty } \frac{a_{n+1}}{a_{n}} = \lim_{n ->\infty } \left[\left(\frac{(n+1)!}{(n+1)^2 cos (n+1)} \div \frac{n!}{n^2 cos (n) }\right)\right]\)

\(\displaystyle = \lim_{n ->\infty} \frac{n^2(n+1)cos(n)}{(n+1)^2cos(n+1)} = \lim_{n ->\infty} \frac{n^2cos(n)}{(n+1)cos(n+1)}\)

\(\displaystyle n^2\) will dominate over \(\displaystyle (n+1)\) since it's a higher order term. Clearly, L will not be less than, which is necessary for absolute convergence. 

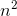
Alternatively, it's clear that \(\displaystyle n!\) is much greater than \(\displaystyle n^2\), and thus having \(\displaystyle n!\) in the numerator will make the series diverge by the \(\displaystyle n^{th}\) limit test (since the terms clearly don't converge to zero).

The other series will converge by alternating series test, ratio test, geometric series, and comparison tests.

First we need to set up our system of equations.

\(\displaystyle 2=2\lambda x \rightarrow x=\frac{1}{\lambda}\)

\(\displaystyle -5=2\lambda y \rightarrow y=-\frac{5}{2 \lambda}\)

\(\displaystyle x^2+y^2=144\)

Now lets plug in these constraints.

\(\displaystyle (\frac{1}{\lambda})^2+(-\frac{5}{2\lambda})^2=144\)

 \(\displaystyle \frac{1}{\lambda ^2}+\frac{25}{4\lambda^2}=144\)

\(\displaystyle \frac{29}{4\lambda^2}=144\)

Now we solve for \(\displaystyle \lambda\)

\(\displaystyle \frac{29}{4\lambda^2}=144\rightarrow \lambda^2=\frac{29}{576}\rightarrow\lambda=\pm\sqrt{\frac{29}{576}}\)

If

 \(\displaystyle \lambda=\sqrt{\frac{29}{576}}\)

\(\displaystyle x=\frac{1}{\sqrt{\frac{29}{576}}}\approx 4.46\), \(\displaystyle y=-\frac{5}{2\sqrt{\frac{29}{576}}}\approx -11.14\)

If

 \(\displaystyle \lambda=-\sqrt{\frac{29}{576}}\)

\(\displaystyle x=\frac{1}{\sqrt{\frac{29}{576}}}\approx -4.46\), \(\displaystyle y=-\frac{5}{2\sqrt{\frac{29}{576}}}\approx 11.14\)

Now lets plug in these values of \(\displaystyle x\), and \(\displaystyle y\) into the original equation.

\(\displaystyle f(4.46,-11.14)=2(4.46)-5(-11.14)=64.62\)

\(\displaystyle f(-4.46,11.14)=2(-4.46)-5(11.14)=-64.62\)

We can conclude from this that \(\displaystyle f(4.46,-11.14)\) is a maximum, and \(\displaystyle f(-4.46,11.14)\) is a minimum.

Let \(\displaystyle g = x^2 +2y^2\)To find the absolute minimum value, we must solve the system of equations given by

\(\displaystyle \triangledown f = \lambda\triangledown g, g =1\).

So this system of equations is

\(\displaystyle f_x = \lambda g_x\), \(\displaystyle f_y = \lambda g_y\), \(\displaystyle g =1\).

Taking partial derivatives and substituting as indicated, this becomes

\(\displaystyle 2x = \lambda(2x), 2y = \lambda(4y), x^2+2y^2 = 1\).

From the left equation, we see either \(\displaystyle x=0\) or \(\displaystyle \lambda = 1\). If \(\displaystyle x=0\), then substituting this into the other equations, we can solve for \(\displaystyle y, \lambda\), and get \(\displaystyle y = \pm \sqrt{2}/2\), \(\displaystyle \lambda = 1/2\), giving two extreme candidate points at \(\displaystyle (0, \frac{\sqrt{2}}{2}), (0, -\frac{\sqrt{2}}{2})\).

On the other hand, if instead \(\displaystyle \lambda =1\), this forces \(\displaystyle y = 0\) from the 2nd equation, and \(\displaystyle x = \pm 1\) from the 3rd equation. This gives us two more extreme candidate points; \(\displaystyle (-1,0),(1,0)\).

Taking all four of our found points, and plugging them back into \(\displaystyle f\), we have

\(\displaystyle f(-1,0) = 1, f(1,0) = 1, f(0,\frac{\sqrt{2}}{2}) = \frac{1}{2}, f(0,-\frac{\sqrt{2}}{2}) = \frac{1}{2}\).

Hence the absolute minimum value is \(\displaystyle \frac{1}{2}\).