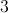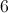Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Integers

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Do Absolute Value In Pre Algebra

Solve the absolute value expression.

$\small \small 6\left | 3-8 \right |+14$

Possible Answers:

Correct answer:

Explanation:

$\small \small 6\left | 3-8 \right |+14$

Simplify the absolute value, as if it were a parenthesis.

$\small \small 6\left | -5 \right |+14$

The absolute value of is . Remember that absolute values are always positive.

$\small (6)(5)+14$

$\small 30+14=44$

Report an Error

Example Question #83 : High School Math

Is the inequality below true or false?

$\small \small \left | -7 \right |>12-6$

Possible Answers:

True

The answer cannot be determined

False; the two terms are equal

False; the sign should be changed to "less than"

Correct answer:

True

Explanation:

An absolute value is always the positive solution.

$\small \left | -7 \right |=7$

We can compare the terms by substituting the positive value of , and solving the right side of the inequality.

$\small \small \small \left | -7 \right |>12-6$

$\small \left | -7 \right |>6$

$\small 7>6$

The inequality is a true expression.

Report an Error

Example Question #5 : How To Do Absolute Value In Pre Algebra

Evaluate $\left | -6+5-2 \right |$

Possible Answers:

Correct answer:

Explanation:

To solve problems with absolute value, first solve inside the absolute value signs. -6+5-2 = -3 .

The absolute value of is because the negative sign is inside the absolute value signs. Remember the absolute value is the distance from that number to zero on the number line. Therefore, the absolute value is always positive.

Report an Error

Example Question #6 : How To Do Absolute Value In Pre Algebra

Evaluate the expression.

$\left | 3-5\right |$

Possible Answers:

Correct answer:

Explanation:

First, treat the absolute value as a parenthesis, and evaluate the term inside.

$\left | 3-5\right |$

$\left | -2\right |$

The absolute value of any term is its distance from zero. A distance cannot be negative, thus, any negative term in an absolute value will be converted to a positive term.

$\left | -2\right |=2$

Report an Error

Example Question #84 : High School Math

$\left |-3 \right |=?$

Possible Answers:

Correct answer:

Explanation:

The absolute value of a number can be thought of as its distance from zero. is three units away from zero. Therefore, $\left |-3 \right |=3$ .

Report an Error

Example Question #8 : How To Do Absolute Value In Pre Algebra

$\left | 3^2-12\right |=?$

Possible Answers:

$\frac{3}{4}$

Correct answer:

Explanation:

The absolute value of a number can be thought of as its distance from zero.

We start by solving the expression inside the absolute value signs and then measure how far that is from zero.

$\left | 3^2-12\right |$

$=\left | 9-12\right |$

$=\left | -3\right |$

is three units away from zero. Therefore, $\left | 3^2-12\right |=\left |-3 \right |=3.$

Report an Error

Example Question #5 : How To Do Absolute Value In Pre Algebra

$\left | -5+3\right |=?$

Possible Answers:

$2\tfrac{1}{2}$

Correct answer:

Explanation:

The absolute value of a number can be thought of as its distance from zero.

We start by solving the expression inside the absolute value signs and then measure how far that is from zero.

$\left | -5+3\right |$

$=\left | -2\right |$

is two units away from zero. Therefore $\left | -5+3\right |=\left | -2\right |=2.$

Report an Error

Example Question #9 : How To Do Absolute Value In Pre Algebra

$\left | 12+24\right |=?$

Possible Answers:

$\frac{1}{2}$

Correct answer:

Explanation:

The absolute value of a number can be thought of as its distance from zero.

We start by solving the expression inside the absolute value signs and then measure how far that is from zero.

$\left | 12+24\right |$

$=\left | 36\right |$

is units away from zero. That means that $\left | 12+24\right |=\left | 36\right |=36.$

Report an Error

Example Question #91 : High School Math

What is |-3| ?

Possible Answers:

Correct answer:

Explanation:

The absolute value of or, mathematically, |-3| , measures the distance between the number and zero. Since is three units away from zero, the absolute value will be .

Report an Error

Example Question #11 : How To Do Absolute Value In Pre Algebra

What is the absolute value of ?

Possible Answers:

Correct answer:

Explanation:

Recall that absolute value describes the distance a number is from . As a result of this, absolute value is always positive. Then, we have that the absolute value of must be .

Report an Error

View Tutors

Elizabeth
Certified Tutor

Clark Atlanta University, Bachelor of Science, Physics. Berry College, Doctor of Education, Curriculum and Instruction.

View Tutors

Tatiana
Certified Tutor

Moscow State Linguistic University, Bachelors, German. Moscow State Linguistic University, PHD, Germanic Languages .

View Tutors

Suley
Certified Tutor

American Public University System, Masters in Education, Curriculum and Instruction.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in San Diego, Reading Tutors in Atlanta, Math Tutors in Seattle, SAT Tutors in Seattle, GRE Tutors in Washington DC, Statistics Tutors in Washington DC, Reading Tutors in San Francisco-Bay Area, French Tutors in Seattle, MCAT Tutors in New York City, Algebra Tutors in Washington DC

Popular Courses & Classes

Spanish Courses & Classes in San Diego, ISEE Courses & Classes in Denver, SAT Courses & Classes in New York City, ISEE Courses & Classes in Houston, ISEE Courses & Classes in Chicago, SSAT Courses & Classes in Boston, GMAT Courses & Classes in Miami, ACT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Seattle, ACT Courses & Classes in Seattle

Popular Test Prep

LSAT Test Prep in Atlanta, SAT Test Prep in Chicago, GRE Test Prep in Los Angeles, LSAT Test Prep in Houston, GMAT Test Prep in Miami, ACT Test Prep in New York City, ACT Test Prep in Seattle, ACT Test Prep in Denver, GMAT Test Prep in Philadelphia, GRE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Integers

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #3 : How To Do Absolute Value In Pre Algebra

Example Question #83 : High School Math

Example Question #5 : How To Do Absolute Value In Pre Algebra

Example Question #6 : How To Do Absolute Value In Pre Algebra

Example Question #84 : High School Math

Example Question #8 : How To Do Absolute Value In Pre Algebra

Example Question #5 : How To Do Absolute Value In Pre Algebra

Example Question #9 : How To Do Absolute Value In Pre Algebra

Example Question #91 : High School Math

Example Question #11 : How To Do Absolute Value In Pre Algebra

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: