Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Middle Level Math : Geometry

Study concepts, example questions & explanations for ISEE Middle Level Math

Create An Account

All ISEE Middle Level Math Resources

6 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #43 : Rectangles

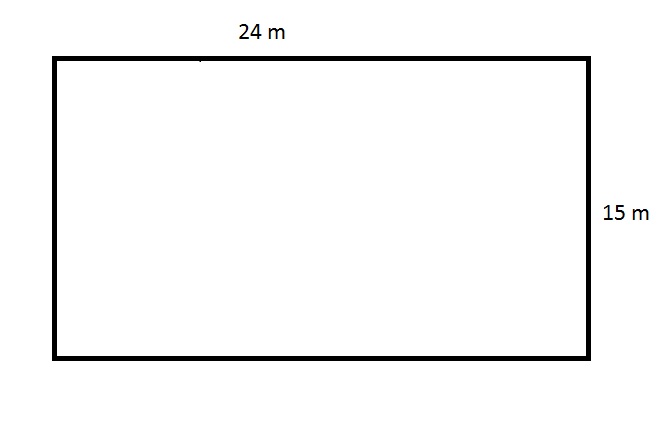
Swimming_pool

The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely, but the store will only sell the material in multiples of one hundred square meters. How many square meters will the manager need to buy?

Possible Answers:

$500\textrm{ m}^{2}$ $\displaystyle 500\textrm{ m}^{2}$

$300\textrm{ m}^{2}$ $\displaystyle 300\textrm{ m}^{2}$

$400\textrm{ m}^{2}$ $\displaystyle 400\textrm{ m}^{2}$

Insufficient information is given to answer the question.

$600\textrm{ m}^{2}$ $\displaystyle 600\textrm{ m}^{2}$

Correct answer:

$400\textrm{ m}^{2}$ $\displaystyle 400\textrm{ m}^{2}$

Explanation:

The tarp needed to cover this pool must be, at minimum, the product of its length and width, or

$24 \times 15 = 360$ $\displaystyle 24 \times 15 = 360$ square meters.

The manager will need to buy a number of square yards of tarp equal to the next highest multiple of one hundred, which is 400 square meters.

Report an Error

Example Question #51 : Rectangles

The four angles of a square are labeled A, B, C, and D. What is the sum of A+B+C $\displaystyle A+B+C$?

Possible Answers:

300^o $\displaystyle 300^o$

180^o $\displaystyle 180^o$

More information is needed to solve

90^o $\displaystyle 90^o$

270^o $\displaystyle 270^o$

Correct answer:

270^o $\displaystyle 270^o$

Explanation:

In a square, each angle is 90 degrees.

$\displaystyle A=B=C=D=90^o$

We can plug in 90 for each variable and find the sum.

$\displaystyle A+B+C=90^o+90^o+90^o=270^o$

Report an Error

Example Question #24 : How To Find The Area Of A Rectangle

Swimming_pool

The above depicts a rectangular swimming pool for an apartment. The pool is six feet deep everywhere.

An apartment manager wants to paint the four sides and the bottom of the swimming pool. How many square feet will he need to paint?

Possible Answers:

The correct answer is not given among the other responses.

$10,500 \textrm{ ft}^{2}$ $\displaystyle 10,500 \textrm{ ft}^{2}$

$4,520 \textrm{ ft}^{2}$ $\displaystyle 4,520 \textrm{ ft}^{2}$

$2,770 \textrm{ ft}^{2}$ $\displaystyle 2,770 \textrm{ ft}^{2}$

$1,020 \textrm{ ft}^{2}$ $\displaystyle 1,020 \textrm{ ft}^{2}$

Correct answer:

$2,770 \textrm{ ft}^{2}$ $\displaystyle 2,770 \textrm{ ft}^{2}$

Explanation:

The bottom of the swimming pool has area

$50 \times 35 = 1,750$ $\displaystyle 50 \times 35 = 1,750$ square feet.

There are two sides whose area is

$50 \times 6 = 300$ $\displaystyle 50 \times 6 = 300$ square feet,

and two sides whose area is

$35 \times 6 = 210$ $\displaystyle 35 \times 6 = 210$ square feet.

Add the areas:

$\displaystyle 1,750 + 300 + 300 + 210 +210=2,770$ square feet.

Report an Error

Example Question #25 : How To Find The Area Of A Rectangle

If the angles of a quadrilateral are equal to $\displaystyle b$, $\displaystyle 2b$, $\displaystyle 3b$, and $\displaystyle 3b$, what is the value of $\displaystyle b$?

Possible Answers:

$\displaystyle 40$

$\displaystyle 50$

$\displaystyle 70$

$\displaystyle 60$

Correct answer:

$\displaystyle 40$

Explanation:

Given that there are 360 degrees in a quadrilateral,

$\displaystyle b+2b+3b+3b=360$

9b=360 $\displaystyle 9b=360$

b=40 $\displaystyle b=40$

Report an Error

Example Question #32 : How To Find The Area Of A Rectangle

What is the value of $\displaystyle w$ if the angles of a quadrilateral are equal to $\displaystyle 50$ degrees, 110 $\displaystyle 110$ degrees, $\displaystyle 80$ degrees, and $\displaystyle 2w$?

Possible Answers:

$\displaystyle 74$

$\displaystyle 62$

$\displaystyle 65$

$\displaystyle 60$

Correct answer:

$\displaystyle 60$

Explanation:

Given that there are 360 degrees in a quadrilateral,

$\displaystyle 50 + 110 +80 + 2w=360$

$\displaystyle 240+2w=360$

2w=120 $\displaystyle 2w=120$

w=60 $\displaystyle w=60$

Report an Error

Example Question #52 : Rectangles

If the length of a rectangle is 7.5 feet and the width is 2 feet, what is the value of $\displaystyle x$ if the area is $\displaystyle 5x$?

Possible Answers:

$\displaystyle 3$

$\displaystyle 15$

$\displaystyle 2$

$\displaystyle 5$

Correct answer:

$\displaystyle 3$

Explanation:

The area of a rectangle is calculated by multiplying the length by the width. Here, the length is 7.5 and the width is 2, so the area will be 15.

Given that the area is also equal to $\displaystyle 5x$, the value of $\displaystyle x$ will be 3, given that 3 times 5 is 15.

Report an Error

Example Question #161 : Geometry

Which of the following is equal to the area of a rectangle with length 4.3 $\displaystyle 4.3$ meters and width 3.5 $\displaystyle 3.5$ meters?

Possible Answers:

$15,500 \textrm{ cm}^{2}$ $\displaystyle 15,500 \textrm{ cm}^{2}$

$155,000 \textrm{ cm}^{2}$ $\displaystyle 155,000 \textrm{ cm}^{2}$

$15,050 \textrm{ cm}^{2}$ $\displaystyle 15,050 \textrm{ cm}^{2}$

$150,500 \textrm{ cm}^{2}$ $\displaystyle 150,500 \textrm{ cm}^{2}$

Correct answer:

$150,500 \textrm{ cm}^{2}$ $\displaystyle 150,500 \textrm{ cm}^{2}$

Explanation:

Multiply each dimension by 100 $\displaystyle 100$ to convert meters to centimeters:

$4.3 \times 100 = 430$ $\displaystyle 4.3 \times 100 = 430$

$3.5 \times 100 = 350$ $\displaystyle 3.5 \times 100 = 350$

Multiply these dimensions to get the area of the rectangle in square centimeters:

$430 \times 350 = 150,500\textrm{ cm}^{2}$ $\displaystyle 430 \times 350 = 150,500\textrm{ cm}^{2}$

Report an Error

Example Question #181 : Geometry

Find the area of a rectangle whose length is 6 and width is 5.

Possible Answers:

$\displaystyle 5$

$\displaystyle 15$

$\displaystyle 30$

$\displaystyle 22$

Correct answer:

$\displaystyle 30$

Explanation:

To solve, simply use the formula for the area of a rectangle.

In this particular case the length and width are given,

$\displaystyle l=6, w=5$.

Thus:

$\displaystyle area=l*w=6*5=30$

Report an Error

Example Question #30 : How To Find The Area Of A Rectangle

The area of a four-sided room that has dimensions of $10\times12$ $\displaystyle 10\times12$ will be the four wall lengths all added to together. True or False?

Possible Answers:

False

True

Correct answer:

False

Explanation:

The area of a rectangle is the length times the width. So to calculate it, you must multiple the two different lengths together. Adding the four wall lengths would get you the perimeter instead.

Report an Error

Example Question #31 : Rectangles

Use the following to answer the question.

Rectangle4

Find the area of the rectangle if it's width is half of it's length.

Possible Answers:

$72\text{ft}^2$ $\displaystyle 72\text{ft}^2$

$36\text{ft}^2$ $\displaystyle 36\text{ft}^2$

$36\text{ft}$ $\displaystyle 36\text{ft}$

$\text{There is not enough information to answer the question.}$ $\displaystyle \text{There is not enough information to answer the question.}$

$72\text{ft}$ $\displaystyle 72\text{ft}$

Correct answer:

$72\text{ft}^2$ $\displaystyle 72\text{ft}^2$

Explanation:

To find the area of a rectangle, we use the following formula:

$\text{area of rectangle} = l \cdot w$ $\displaystyle \text{area of rectangle} = l \cdot w$

where l is the length and w is the width of the rectangle.

Now, given the rectangle,

Rectangle4

we can see the length is 12 feet. We also know the width is half of the length. Therefore, the width is 6 feet. Knowing this, we can substitute into the formula. We get

$\text{area of rectangle} = 12\text{ft} \cdot 6\text{ft}$ $\displaystyle \text{area of rectangle} = 12\text{ft} \cdot 6\text{ft}$

$\text{area of rectangle} = 72\text{ft}^2$ $\displaystyle \text{area of rectangle} = 72\text{ft}^2$

Report an Error

View Tutors

Clarissa
Certified Tutor

University of North Texas, Bachelor in Arts, International Relations.

View Tutors

Cheryl
Certified Tutor

Palm Beach Atlantic University-West Palm Beach, Bachelor of Science, Business Administration and Management. Southern New Ham...

View Tutors

Iffy
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Engineering, General. University of Maryland-College P...

All ISEE Middle Level Math Resources

6 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Dallas Fort Worth, ISEE Tutors in Seattle, Biology Tutors in Seattle, ISEE Tutors in Denver, Statistics Tutors in New York City, Reading Tutors in Seattle, SSAT Tutors in Miami, LSAT Tutors in Los Angeles, LSAT Tutors in Philadelphia, Chemistry Tutors in Denver

Popular Courses & Classes

SSAT Courses & Classes in Chicago, SSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Houston, MCAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Phoenix, ISEE Courses & Classes in Philadelphia, GMAT Courses & Classes in Denver, SSAT Courses & Classes in Seattle, SAT Courses & Classes in Seattle, SAT Courses & Classes in Philadelphia

Popular Test Prep

GMAT Test Prep in Boston, GMAT Test Prep in Houston, GMAT Test Prep in San Diego, LSAT Test Prep in Phoenix, ISEE Test Prep in Washington DC, SSAT Test Prep in San Diego, SSAT Test Prep in Washington DC, ACT Test Prep in Washington DC, GMAT Test Prep in Atlanta, GRE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Middle Level Math : Geometry

Study concepts, example questions & explanations for ISEE Middle Level Math

All ISEE Middle Level Math Resources

Example Questions

Example Question #43 : Rectangles

Example Question #51 : Rectangles

Example Question #24 : How To Find The Area Of A Rectangle

Example Question #25 : How To Find The Area Of A Rectangle

Example Question #32 : How To Find The Area Of A Rectangle

Example Question #52 : Rectangles

Example Question #161 : Geometry

Example Question #181 : Geometry

Example Question #30 : How To Find The Area Of A Rectangle

Example Question #31 : Rectangles

All ISEE Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: