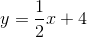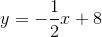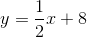Start by changing the less than sign to an equal sign and solve for .

Now, plot these two numbers on a number line.

Notice how the number line is divided into three regions:

Now, choose a number fromeach of these regions to plug back into the inequality to test if the inequality holds.

For , let 

Since this number is not less than zero, the solution cannot be found in this region.

For , let 

Since this number is less than zero, the solution can be found in this region.

For  let .

Since this number is not less than zero, the solution cannot be found in this region.

Because the solution is only negative in the interval , that must be the solution.

First, we can factor the quadratic to give us a better understanding of its graph. Factoring gives us: . Now we know that the quadratic has zeros at  and . Furthermore this information reveals that the quadratic is positive. Using this information, we can sketch a graph like this: 

We can see that the parabola is below the x-axis (in other words, less than ) between these two zeros  and .

The only x-value satisfying the inequality  is .

The value of  would work if the inequality were inclusive, but since it is strictly less than instead of less than or equal to , that value will not work.

The best way to simplify a radical within a radical is to rewrite each root as a fractional exponent, then convert back.

First, rewrite the roots as exponents.

Multiply the exponents, per the power of a power rule:

Define 

Then if ,

it follows that

,

or, equivalently,

.

By the Intermediate Value Theorem (IVT), if  is a continuous function, and  and  are of unlike sign, then  for some . As a polynomial,  is a continuous function, so the IVT applies here.

Evaluate  for each of the following values: :

Only in the case of  does it hold that  assumes a different sign at both endpoints - . By the IVT, , and , for some .

First, we need to find the slope of the above line. 

The slope of a line. given two points  can be calculated using the slope formula

Set :

The slope of a line perpendicular to it has as its slope the opposite of the reciprocal of 2, which would be . Since we want this line to have the same -intercept as the first line, which is the point , we can substitute  and  in the slope-intercept form:

One way to answer this is to first find the equation of the line. 

The slope of a line. given two points  can be calculated using the slope formula

Set :

The line has slope 3 and -intercept , so we can substitute  in the slope-intercept form:

Now substitute 4 for  and  for  and solve for :

To find an equation of a line, we will always need to know the slope of that line -- and to find the slope, we need at least two points. It looks like we have (0, -3) and (12,0), which we'll call point 1 and point 2, respectively.

Now we need to plug in a point on the line into an equation for a line. We can use either slope-intercept form or point-slope form, but since the answer choices are in point-slope form, let's use that.

Unfortunately, that's not one of the answer choices. That's because we didn't pick the same point to substitute into our equation as the answer choices did. But we can see if any of the answer choices are equivalent to what we found. Our equation is equal to:

which is the slope-intercept form of the line. We have to put all the other answer choices into slope-intercept to see if they match. The only one that works is this one:

We can solve the system of equations using the substitution method.

Solve for  in the second equation.

Substitute this value of  into the first equation.

Now we can solve for .

Solve for  using the first equation with this new value of .

The solution is the ordered pair .

First, we need to find the slope of the line.

In order to move from the lower left point to the upper right point, it is necessary to move up five units and right three units. This is a rise of 5 and a run of 3. makes the slope of the line shown .

We can use this to find the -intercept  using the slope formula as follows:

The lower left point has coordinates . Therefore, we can set up and solve for  in this slope formula, setting :

We calculate the slopes of the lines using the slope formula.

The slope of line  is 

The slope of line  is 

The lines have the same slope, making them either parallel or identical.

Since the slope of each line is 0, both lines are horizontal, and the equation of each takes the form , where  is the -coordinate of each point on the line. Therefore, line  and line  have equations  and .This makes them parallel lines.