All SAT II Math I Resources
Example Questions
Example Question #21 : Parabolic Functions
Find the vertex form of the following quadratic equation:
Factor 2 as GCF from the first two terms giving us:
Now we complete the square by adding 4 to the expression inside the parenthesis and subtracting 8 ( because 
which is equal to
Hence the vertex is located at
Example Question #1 : Graphing Parabolas
None of them
Purple line
Red line
Blue line
Green line
Red line
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to 
The blue line represents a linear function and will have a formula similar to 
The green line represents an exponential function and will have a formula similar to 
The purple line represents an absolute value function and will have a formula similar to 
Example Question #8 : Graphing Quadratic Functions
Which of the following parabolas is downward facing?
We can determine if a parabola is upward or downward facing by looking at the coefficient of the 



Example Question #2 : Graphing Parabolas
What is the vertex of the function 





The equation of a parabola can be written in vertex form: 
The point 


In this example, 
Example Question #10 : Graphing Quadratic Functions
How many points of intersection could two distinct quadratic functions have?











An intersection of two functions is a point they share in common. A diagram can show all the possible solutions:

Notice that:









The diagram shows that 


Example Question #1 : Graphing Parabolas
Which of the following graphs matches the function 






Start by visualizing the graph associated with the function :

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of looks like this:

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function :

Example Question #21 : Graphing Functions
Simplify the following expression:
To simplify, we must first simplify the absolute values.
Now, combine like terms:
Example Question #1 : Graphing Polynomial Functions
Where does 

5
-7
7
-3
3
7




Example Question #142 : Functions And Graphs

Which of the following is an equation for the above parabola?
The zeros of the parabola are at 


each of their signs is reversed to end up with the correct sign in the answer. The coefficient can be found by plugging in any easily-identifiable, non-zero point to the above formula. For example, we can plug in 

Example Question #581 : Functions And Graphs
Which equation best represents the following graph?
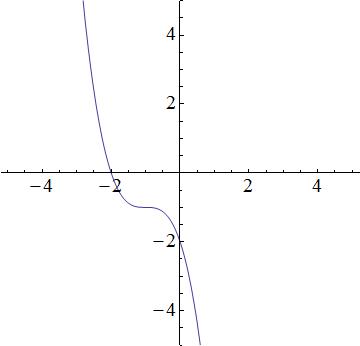
None of these
We have the following answer choices.
The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
Certified Tutor
All SAT II Math I Resources



















































