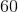All SAT Math Resources
Example Questions
Example Question #711 : Arithmetic
If 
Since v is divisible by 2, 3 and 15, v must be a multiple of 30. Any number that is divisible by both 2 and 15 must be divisible by their product, 30, since this is the least common multiple.
Out of all the answer choices, v + 30 is the only one that equals a multiple of 30.
Example Question #712 : Arithmetic
Suppose that 



We are given information that m/4 is 10 greater than m/3. We set up an equation where m/4 = m/3 + 10.
We must then give the m variables a common denominator in order to solve for m. Since 3 * 4 = 12, we can use 12 as our denominator for both m variables.
m/4 = m/3 + 10 (Multiply m/4 by 3 in the numerator and denominator.)
3m/12 = m/3 + 10 (Multiply m/3 by 4 in the numerator and denominator.)
3m/12 = 4m/12 + 10 (Subtract 4m/12 on both sides.)
-m/12 = 10 (Multiply both sides by -12.)
m = -120
-120/4 = -30 and -120/3 = -40. -30 is 10 greater than -40.
Example Question #713 : Arithmetic



The greatest common divisor of 

The greatest common divisor of 

The greatest common divisor of 

If 
The greatest common divisor of 



The greatest common divisor of 



The greatest common divisor of 



Thus:
We substitute these equalities into the given expression and simplify.
Since 










Therefore:
or
Example Question #714 : Arithmetic
What's the greatest common factor of 6 and 8?
Greatest common factor is a common factor shared by two or more numbers. Both numbers are even, so let's divide both numbers by two. We get 

Example Question #5 : How To Find The Greatest Common Factor
What's the greatest common factor of 4 and 8?
Greatest common factor is a common factor shared by two or more numbers. 




Example Question #21 : Factors / Multiples
What's the greatest common factor of 19 and 27?
Greatest common factor is a common factor shared by two or more numbers. 


Example Question #22 : Factors / Multiples
What's the greatest common factor of 24 and 74?
Greatest common factor is a common factor shared by two or more numbers. Both numbers are even, so let's divide two for both numbers. We get 

Example Question #8 : How To Find The Greatest Common Factor
What's the greatest common factor of 18 and 243?
Greatest common factor is a common factor shared by two or more numbers. If you know the divisibility rule of 










Example Question #1 : How To Find The Greatest Common Factor
What's the greatest common factor of 33 and 121?
Greatest common factor is a common factor shared by two or more numbers. If you know divisibility rule of 

















Example Question #10 : How To Find The Greatest Common Factor
What's the greatest common factor of 55 and 80?
These two numbers are definitely divisible by 




All SAT Math Resources