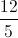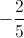All SSAT Middle Level Math Resources
Example Questions
Example Question #1 : Geometry
Give the slope of the line that passes through 

Use the slope formula, substituting 
Example Question #182 : Ssat Middle Level Quantitative (Math)
Give the slope of a line that passes through 

Using the slope formula, substituting 



Subtract to get:
Cancel out the negative signs to get:
Example Question #2 : Geometry
Give the slope of a line that passes through 

Using the slope formula with 



Subtract to get:

Example Question #3 : Geometry
Give the slope of the line that passes through 

Using the slope formula for




Combine the negative signs to get:
Subtract and add to get:
Reduce to get:
Example Question #2 : Geometry
Give the slope of a line that passes through 

Using the slope formula, where 




Example Question #1 : Geometry
Find the slope of the line that passes through the points 
Cannot be determined
Using the slope formula, where 




Example Question #1 : Geometry
Find the slope of a line with points 

Cannot be determined
Using the slope formula, where 




Example Question #432 : Hspt Mathematics
Billy set up a ramp for his toy cars. He did this by taking a wooden plank and putting one end on top of a brick that was 3 inches high. He then put the other end on top of a box that was 9 inches high. The bricks were 18 inches apart. What is the slope of the plank?
The value of the slope (m) is rise over run, and can be calculated with the formula below:
The coordinates of the first end of the plank would be (0,3), given that this is the starting point of the plank (so x would be 0), and y would be 3 since the brick is 3 inches tall.
The coordinates of the second end of the plank would be (18,9) since the plank is 18 inches long (so x would be 18) and y would be 9 since the box was 9 inches tall at the other end.
From this information we know that we can assign the following coordinates for the equation:

Below is the solution we would get from plugging this information into the equation for slope:
This reduces to
Example Question #5 : Geometry
Find the area of the above triangle, given that it has a height of 12 and a base of 10.
Because this is a right triangle, the area formula is simply:
Thus, the solution is:
Example Question #6 : Geometry
Given the above triangle is an equilateral triangle, find the perimeter in units as drawn in the coordinate system.
Using the coordinate system, one can see the base of the triangle is 6 units in length. Since it is an equilateral triangle, the other two sides must also be 6 units each in length. Therefore the perimeter is:
Certified Tutor
All SSAT Middle Level Math Resources