All SSAT Middle Level Math Resources
Example Questions
Example Question #206 : Ssat Middle Level Quantitative (Math)
Which of the following points is in Quadrant II on the coordinate plane?
All points in Quadrant II have negative 


Example Question #207 : Ssat Middle Level Quantitative (Math)
In which quadrant or on which axis will we find the point 
Quadrant IV
The 
The 
Quadrant II
Quadrant I
The 
By definition, any point in the coordinate plane that has a non-zero value 


Example Question #208 : Ssat Middle Level Quantitative (Math)
In which quadrant or on which axis of the coordinate plane will you find the point 
The 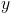
Quadrant I
Quadrant II
Quadrant IV
Quadrant III
Quadrant IV
A point with a positive 

Example Question #4 : How To Find The Points On A Coordinate Plane
A line segment on the coordinate plane has its endpoints at the points with coordinates 

The 

The 
The coordinates of the midpoint are 
Example Question #8 : How To Find The Points On A Coordinate Plane
A line segment on the coordinate plane has its endpoints at the points with coordinates 

The 

The 
The midpoint has coordinates 
Example Question #21 : Geometry
In which quadrant or on which axis will you find the point 
Quadrant IV
Quadrant II
Quadrant III
Quadrant I
The 
Quadrant III
By definition, a point with a negative 

Example Question #212 : Ssat Middle Level Quantitative (Math)

The above square has an area of 
To find the fraction of the entire squares area that lays in quadrant II, notice that the square is taking up an equivalent amount in each of the four quadrants. Thus, 
Also note that the area of the square that lays in quadrant II is 

Example Question #26 : Geometry
If a square has an area of 
In order to solve this problem, apply the formula 



Once you've found the length of side 

Thus, the solution is
Example Question #27 : Geometry
A square has an area of 

In order to solve this problem, apply the formula 



Once you've found the length of side 
Example Question #28 : Geometry

Find the perimeter of the square shown above.
To find the perimeter of this square, apply the formula: 

Thus, the solution is:
Certified Tutor
Certified Tutor
All SSAT Middle Level Math Resources










![\left [(-10 ) + (-20) \right ] \div 2 = \left [-(10 + 20) \right ] \div 2 = -30 \div 2 = -15](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/734440/gif.latex)
![\left [ (-20)+ 10 \right ] \div 2 = \left [-(20-10) \right ] \div 2 = -10 \div 2 = -5](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/734441/gif.latex)





































