All SSAT Middle Level Math Resources
Example Questions
Example Question #74 : Quadrilaterals
The length of a rectangle is three times longer than its width. If the width of the rectangle is 
The length of the rectangle would be:
We know that:
where:
So we can write:
Example Question #75 : Quadrilaterals
Which of the following is the area of a rectangle with a width of 4 feet and a length that is twice the width?
The area of a rectangle is found by multiplying the width by the length.
We know that the width is 4 feet and the the length must be twice the width. Multiply the width by 2 to find the length.
Multiply the length and width to find the area.
Example Question #153 : Geometry
Jeff decided to build a play area for his guinea pigs. The play area would be an enclosure 6 feet long, 2 feet wide, and 2 feet tall. In cubic feet, how big is the play area?
The cubic feet of an area is found by multiping the length times the width times the height. Given that the length is six feet, the width is two feet, and that the height is two feet, the total cubic area would be found using this equation:
Here is the equation with the appropriate numbers plugged in:
Therefore, 24 cubic feet is the correct answer.
Example Question #71 : Quadrilaterals
Jessica's blanket is 12 square feet. Lisa has a blanket that is half the size of Jessica's blanket. Which of the following are possible dimensions of Lisa's blanket?
The area of a rectangle if found by multiplying the length times the width. Here, we know that Lisa's blanket is half the area of Jessica's blanket. Since Jessica's blanket is 12 square feet, that means that Lisa's blanket must be 6 square feet.
The only length and width values that give us 6 square feet when multiplied by one another are 3 feet by 2 feet. This is therefore the correct answer.
Example Question #11 : How To Find The Area Of A Rectangle

Note: Figure NOT drawn to scale.
What percent of the above figure is red?
The correct answer is not given among the other choices.
The correct answer is not given among the other choices.
The large rectangle has length 80 and width 40, and, consequently, area

The white region is a rectangle with length 30 and width 20, and, consequently, area

The red region, therefore, has area 
The red region is
of the large rectangle.
This is not one of the choices.
Example Question #21 : How To Find The Area Of A Rectangle

Note: Figure NOT drawn to scale.
Refer to the above diagram. Give the ratio of the area of the red region to that of the white region.
The correct answer is not given among the other choices.
The large rectangle has length 80 and width 40, and, consequently, area

The white region is a rectangle with length 30 and width 20, and, consequently, area

The red region, therefore, has area 
The ratio of the area of the red region to that of the white region is
That is, 13 to 3.
Example Question #22 : How To Find The Area Of A Rectangle
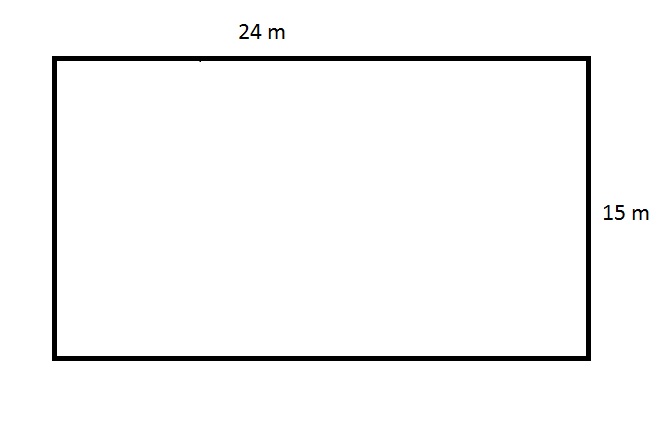
The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely, but the store will only sell the material in multiples of one hundred square meters. How many square meters will the manager need to buy?
Insufficient information is given to answer the question.
The tarp needed to cover this pool must be, at minimum, the product of its length and width, or

The manager will need to buy a number of square yards of tarp equal to the next highest multiple of one hundred, which is 400 square meters.
Example Question #72 : Quadrilaterals
The four angles of a square are labeled A, B, C, and D. What is the sum of 
More information is needed to solve
In a square, each angle is 90 degrees.
We can plug in 90 for each variable and find the sum.
Example Question #52 : Rectangles

The above depicts a rectangular swimming pool for an apartment. The pool is six feet deep everywhere.
An apartment manager wants to paint the four sides and the bottom of the swimming pool. How many square feet will he need to paint?
The correct answer is not given among the other responses.
The bottom of the swimming pool has area

There are two sides whose area is

and two sides whose area is

Add the areas:

Example Question #53 : Rectangles
If the angles of a quadrilateral are equal to 




Given that there are 360 degrees in a quadrilateral,
Certified Tutor
All SSAT Middle Level Math Resources































































