$\displaystyle x+y< 12$ is the correct answer, because the only thing the problem tells us is that the sweet potatoes and onions add up to a number less than 12. It does not say if one is more than the other, and does not say it could equal 12. Therefore the less than sign should not be underlined. 

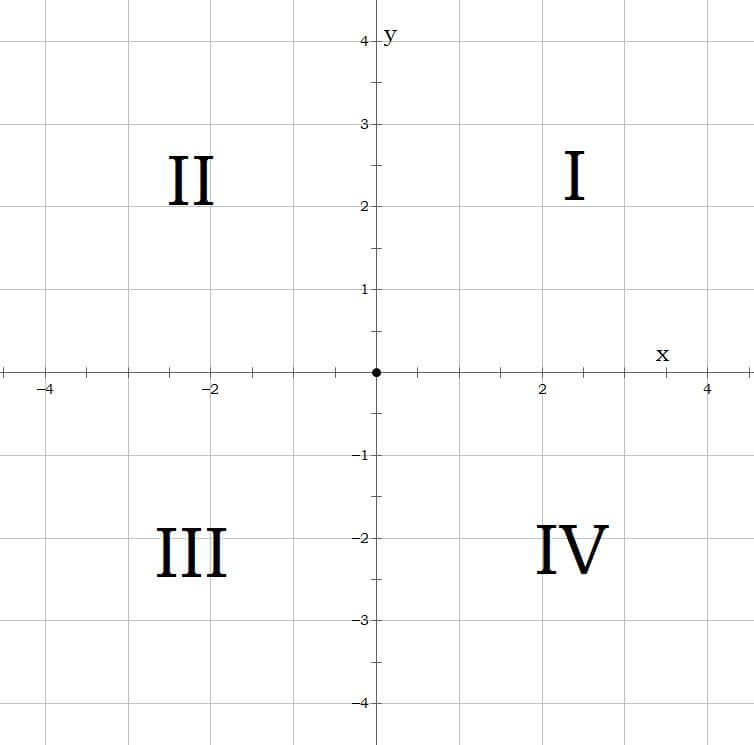
Because x is greater than zero, it will be to the right of the y axis. Because y is less than zero, it will be below the x axis. This is the fourth quadrant. 

For the player to lose, the host has to guess within $\displaystyle 3$ pounds of the player's weight, inclusive. Thus, the host can guess any number between $\displaystyle 142$ pounds $\displaystyle (145-3)$ and $\displaystyle 148$ pounds $\displaystyle (145+3)$; that is, if $\displaystyle x$ is the weight the host guesses, then $\displaystyle \small \small -3\leq x-145 \leq 3$, which translates to $\displaystyle \small |x-145| \leq 3$. 

Split up the inequality into parts.

A number squared:  $\displaystyle x^2$

Three times a number squared:  $\displaystyle 3x^2$

Four less than three times a number squared:  $\displaystyle 3x^2-4$

Is at least six:  $\displaystyle \geq6$

Combine all the parts to form an inequality:  $\displaystyle 3x^2-4\geq6$

The answer is:  $\displaystyle 3x^2-4\geq6$

Break up the sentence into parts.

A number less than five:  $\displaystyle 5-x$

The quantity of a number less than five:  $\displaystyle (5-x)$

Four times the quantity of a number less than five:  $\displaystyle 4(5-x)$

More than six:  $\displaystyle >6$

Combine the terms.

The answer is:  $\displaystyle 4(5-x)>6$

Break up the inequality into parts.

Three times a number:  $\displaystyle 3x$

Two less than three times a number:  $\displaystyle 3x-2$

The quantity of two less than three times a number:  $\displaystyle (3x-2)$

Four times the quantity of two less than three times a number:  $\displaystyle 4(3x-2)$

Is at most ten:  $\displaystyle \leq10$

Combine the terms to form the inequality.

The answer is:  $\displaystyle 4(3x-2)\leq10$

Split up the inequality into parts.

Five times a number:  $\displaystyle 5x$

Two less than five times a number:  $\displaystyle 5x-2$

The quantity of two less than five times a number:  $\displaystyle (5x-2)$

The product of two and the quantity of two less than five times a number:

$\displaystyle 2(5x-2)$

Must exceed twelve: $\displaystyle >12$

The answer is:  $\displaystyle 2(5x-2)>12$

Break up the sentence into parts.  Start with the inner quantity.

Twice a number:  $\displaystyle 2x$

Three less than twice a number:  $\displaystyle 2x-3$

The quantity of three less than twice a number:  $\displaystyle (2x-3)$

Twice the quantity of three less than twice a number:  $\displaystyle 2(2x-3)$

Must be more than ten:  $\displaystyle >10$

Combine the terms to write the inequality: 

The answer is:  $\displaystyle 2(2x-3)>10$

Break up the statement into parts.

The square root of a number:  $\displaystyle \sqrt{x}$

Six times the square root of a number:  $\displaystyle 6\sqrt{x}$

Four less than six times the square root of a number:  $\displaystyle 6\sqrt{x}-4$

At least five:  $\displaystyle \geq5$

Combine the parts to form the inequality.

The answer is:  $\displaystyle 6\sqrt{x}-4\geq5$

Separate the sentence into parts and let the unknown number be $\displaystyle x$.

Eight times a number:  $\displaystyle 8x$

Five more than eight times a number:  $\displaystyle 8x+5$

Must exceed fourteen:  $\displaystyle >14$

Combine the parts to form the inequality.

The answer is:  $\displaystyle 8x+5>14$