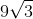All Basic Geometry Resources
Example Questions
Example Question #32 : Geometry
The length of one leg of an equilateral triangle is 6. What is the area of the triangle?
The base is equal to 6.
The height of an quilateral triangle is equal to 

Example Question #1 : How To Find The Area Of A Right Triangle
Find the area of the following right triangle to the nearest integer 
Note: The triangle is not necessarily to scale
None of the other answers
The equation used to find the area of a right triangle is: 

Using the given information, we can write 


Example Question #14 : How To Find The Area Of A Right Triangle
Find the area of this right triangle:
The area of a triangle is 


Now we have our "base" and "height" and we can plug them into the formula to find the area:


Example Question #1401 : Plane Geometry
Find the area of this right triangle:
The area of a triangle is found using the formula 
In this case, we only know one leg, but we can figure out the other by using the Pythagorean Theorem:




Now that we have our "base" and "height," we can substitute them into the formula and find the area:
Example Question #223 : Right Triangles
Find the area of a right triangle whose perpendicular sides are of lengths 

To find area of this triangle, you must use the formula indicated below.
where 

Example Question #222 : Right Triangles
Find the area of a right triangle with leg lengths of 

Recall how to find the area of a right triangle:
Because the legs of the right triangle form a right angle, the legs are also the base and the height.

To find the area of the right triangle, just plug in the values for the lengths of the legs into the equation given above.
Simplify.
Solve.
Example Question #21 : How To Find The Area Of A Right Triangle
Find the area of a right triangle with leg lengths of 

Recall how to find the area of a right triangle:
Because the legs of the right triangle form a right angle, the legs are also the base and the height.

To find the area of the right triangle, just plug in the values for the lengths of the legs into the equation given above.
Simplify.
Solve.
Example Question #421 : Triangles
Find the area of a right triangle with leg lengths of 

Recall how to find the area of a right triangle:
Because the legs of the right triangle form a right angle, the legs are also the base and the height.

To find the area of the right triangle, just plug in the values for the lengths of the legs into the equation given above.
Simplify.
Solve.
Example Question #223 : Right Triangles
Find the area of a right triangle with leg lengths of 

Recall how to find the area of a right triangle:
Because the legs of the right triangle form a right angle, the legs are also the base and the height.

To find the area of the right triangle, just plug in the values for the lengths of the legs into the equation given above.
Simplify.
Solve.
Reduce.
Example Question #1401 : Basic Geometry
Find the area of a right triangle with leg lengths of 

Recall how to find the area of a right triangle:
Because the legs of the right triangle form a right angle, the legs are also the base and the height.

To find the area of the right triangle, just plug in the values for the lengths of the legs into the equation given above.
Simplify.
Solve.
Reduce.
Certified Tutor
All Basic Geometry Resources