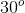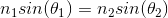MCAT Physical : MCAT Physical Sciences
Study concepts, example questions & explanations for MCAT Physical
All MCAT Physical Resources
Example Questions
Example Question #1 : Snell's Law
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
Red light is selected for by the prism and shown onto the glass cuvette at an angle of 30o to the normal. At what angle to normal does the light travel when it is in the solution after it has moved through wall of the cuvette?
19.5o
22.7o
35o
45o
22.7o
Notice that, in this problem, there are two different changes in indices of refraction: air to glass and glass to solution; thus, we need to compute the angle change twice. First, let’s look at how the angle changes from air to glass. We know from Snell’s law that 
Rearranging, we can find the angle to normal in the glass.
Now, we can use this angle and repeat the above equation to find the angle that the light enters the solution.
Example Question #2 : Snell's Law
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
If the solution had a higher protein concentration than expected, how would the angle of refraction change as light travels from the glass into the solution?
It would be larger
It would be larger or smaller, depending on the color of the light
It would be smaller
It would remain the same
It would be smaller
This question is asking us to consider what would happen if the solution were more concentrated, essentially, if there were more particles per unit volume (denser). If we think back to the definition of index of refraction, we know that it relates to the density of a medium. The denser the medium, the higher the index of refraction.
Looking at Snell’s law, we can see the relationship between index of refraction and the angle of refraction.
If the solution were more concentrated, n2 would increase, making the term on the right side of the equation smaller. The sin function of a smaller number gives a smaller angle; thus, as the concentration increases (and thus the index of refraction increases), the angle of refraction gets smaller.
Example Question #2 : Snell's Law
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
At what angle would the light passing through the glass cuvette need to hit the solution inside the cuvette for no light to enter the solution?
First, we need to determine what this question is asking us to do. If no light entered the solution from the glass, we know this is total internal reflection. Remember that total internal reflection occurs when light from one medium hits a second medium at an angle higher that the critical angle. Thinking back to our physics formulas, we know that the critical angle can be determined by the equation below.
Plugging in the values for glass and the solution, we can find the critical angle.
Example Question #211 : Mcat Physical Sciences
A scuba diver wearing a head lamp is returning to the surface of the Pacific Ocean. What is the index of refraction of the ocean water if the smallest angle resulting in total internal reflection is 35 degrees from the vertical?
We can use Snell's law to calculate the index of refraction of the water:
Where the subscript 1 denotes water and subscript 2 denotes air.
At the first incidence of total internal reflection, the angle of refraction is 90 degrees. Therefore, the sine function becomes 1, giving us the formula:
Rearranging for the index of water:
Example Question #11 : Work, Energy, And Power
A 5kg ball is attached to a 10m rope. The ball is held at a horizontal angle and allowed to fall freely with a pendulum-like motion. Assume there is no air resistance.
What is the velocity of the ball when it is at its lowest point?
This problem becomes much easier if we use the law of conservation of energy. Because there is no friction involved, all of the ball's potential energy was converted into kinetic energy when falling through the pendulum arc. As a result, the velocity at the bottom of the swing can be determined using the equation below.
Because the potential energy at the bottom of the swing is zero (relative to the starting point), and the velocity at the top is zero, we can simplify the equation.
Since the string is 10m long, we know that the lowest point will be 10m below the starting point.
Example Question #21 : Work, Energy, And Power
Two children are playing with sleds on a snow-covered hill. Sam weighs 50kg, and his sled weighs 10kg. Sally weighs 40kg, and her sled weighs 12kg. When they arrive, they climb up the hill using boots. Halfway up the 50-meter hill, Sally slips and rolls back down to the bottom. Sam continues climbing, and eventually Sally joins him at the top.
They then decide to sled down the hill, but disagree about who will go first.
Scenario 1:
Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.
Scenario 2:
Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.
Scenario 3:
Unable to agree, Sam and Sally tether themselves with a rope and go down together.
If the hill is frictionless, and after both Sally and Sam reach the bottom of the hill traveling at maximum velocity, who has lost more potential energy?
Sam, because he is traveling more slowly
Sally, because she is traveling faster
They have lost an equal amount of potential energy
Sally, because she experiences less friction
Sam, because his mass is larger
Sam, because his mass is larger
When they reach the bottom of the hill, Sam and Sally have both converted all of their potential energy into kinetic energy. We measured potential energy at 50m, so once they have lost 50m, the potential energy is 0, while the kinetic energy has reached maximum value. Because Sam has greater mass, he had more potential energy to convert to kinetic energy.
Example Question #41 : Newtonian Mechanics And Motion
Two children are playing with sleds on a snow-covered hill. Sam weighs 50kg, and his sled weighs 10kg. Sally weighs 40kg, and her sled weighs 12kg. When they arrive, they climb up the hill using boots. Halfway up the 50-meter hill, Sally slips and rolls back down to the bottom. Sam continues climbing, and eventually Sally joins him at the top.
They then decide to sled down the hill, but disagree about who will go first.
Scenario 1:
Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.
Scenario 2:
Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.
Scenario 3:
Unable to agree, Sam and Sally tether themselves with a rope and go down together.
After reaching maximum velocity at the bottom of a frictionless hill identical to the one in the question, Sam deploys a parachute. How much energy must the parachute dissipate before Sam comes to a stop?
300J
30kJ
30000kJ
30J
300kJ
30kJ
The parachute must dissipate all of the kinetic energy that Sam has at the bottom of the hill, since there is no friction to slow him. He has 30kJ of energy, as per the equation PE = mgh.
PE = 60kg * 10m/s2 * 50m = 30,000J = KE at the bottom of the hill
Example Question #41 : Newtonian Mechanics And Motion
How much energy is required to a accelerate a 
From an energy stand-point, the block starts with zero kinetic energy and zero potential energy. At the end, the block still has zero potential energy, but has a non-zero kinetic energy. Assuming there is no friction, all energy added to the block have been converted to kinetic energy.
Using the change in velocity, we can solve for the energy used to move the block.
We are given our mass and the change in velocity, allowing us to solve for the change in kinetic energy.
Example Question #22 : Work, Energy, And Power
What is the kinetic energy of a 
Kinetic energy is given by the formula:
We are given the mass of the bullet and its velocity, allowing us to calculate kinetic energy from this formula.
Work is often expressed in Newton-meters, but energy is usually expressed as Joules, although the units are equivalent.
Example Question #1 : Kinetic Energy
Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 
Collision 3:
The two children collide while traveling in opposite directions at 
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of 
In collision 1, imagine that child 2 was not present on the ice. How much energy would child 1 have to dissipate to the lake surface before he came to a stop? Ignore wind resistance.
The amount of kinetic energy that child 1 has after she reaches the lake surface is the amount of energy she will dissipate to the lake before coming to a complete stop.
Certified Tutor
All MCAT Physical Resources
