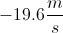Conservation of energy dictates that the initial energy and final energy will be equal.

In this case, the boulder starts with zero kinetic energy and ends with both kinetic and potential energy.

We can cancel the mass from each term and plug in the given values to solve for the velocity at a height of .

Momentum is always conserved in a system, when not experiencing external forces.

An inelastic collision can be identified if the two objects stick together after the collision occurs, such as the bullet becoming embedded in the wood. In an inelastic collision, kinetic energy is not conserved. Since mechanical energy is the sum of kinetic and potential energy, mechanical energy is also not conserved. This lack of conservation is due to the conversion of some of the kinetic energy to heat and sound. The kinetic energy decreases as the heat energy increases, resulting in a non-constant temperature.

We can compare height and velocity by comparing the equations for potential and kinetic energy. This is possible because the rock initially has no kinetic energy (velocity is zero) and has no potential energy upon impact (height is zero). Using conservation of energy will yield the comparison below.

Because velocity is squared in the equation for kinetic energy, it requires a quadrupling of height in order to double the velocity. 

4. Choice 1 is correct because initially, all of the mechanical energy in the stone was potential energy and none was kinetic energy:  ME = KE + PE.  PE is “stored” in the stone-hill system by rolling the stone up hill.  It is obvious that it takes half as much energy to roll the stone half way up the hill, compared with rolling it to the top.  At the bottom of the hill, all of the PE will have been converted into KE, given by the formula  

Since the PE was ½ mgh when rolling the stone half way up hill, it is the same as it rolls down hill.

We need the equation for conservation of energy for this problem:

We can eliminate final potential energy if we set the final height to be zer. We are solving for final velocity, so let's rearrange for final kinetic energy.

Substituting our equations for each variable, we get:

Rearranging for final velocity we get:

If you derive this formula and are unsure of your work, simply check your units. Each term under the square root has units of , which will ultimately give us units of , which is what we want.

We have values for all variables except two: height and normal force.

Let's calculate the height. We know that the between the initial and final states, the cart has traveled 20 meters down a slope of 40 degrees. Therefore, we can calculate height with the formula:

Now we just need to find the normal force. The following diagram will help visualize this calculation.

If you are unsure whether to use sine or cosine, think about it practically. As the angle gets less and less, the normal force is going to get larger. This is characteristic of a cosine function.

Therefore, we can say that:

Now that we have all of our variables, it's time to plug and chug:

Remember that Newton’s second law is applicable regardless of whether we are talking about kinematics, torque, electric, magnetic, or gravitational force, thus, F = ma. We know that the only force acting in free-fall in an environment where we can neglect air resistance (i.e. most of the problems on the MCAT) is gravity. The acceleration due to gravity is 9.8m/s². The sign could be + or – depending on how you decided to orient.

We are given the time that the ball is in the air and the acceleration. Since the ball is dropped, we can also tell that the initial velocity is zero (starts from rest). Using these given values, we can calculate the final velocity using the appropriate motion equation.

The resulting displacement is negative because the ball is traveling downward; however, the height will be the absolute value of the displacement, giving out final answer.

We are given the time that the ball is in the air and the acceleration. Since the ball is dropped, we can also tell that the initial velocity is zero (starts from rest). Using these given values, we can calculate the final velocity using the appropriate motion equation.

The final velocity is negative because the ball is traveling downward; however, the question asks for speed, allowing us to disregard the vector indicator. Speed cannot be negative.

The question tells us that the initial velocity of the ball (v₀) is zero and the height (d) of the cliff is 80m. Acceleration (gravity) is 10m/s². Using the kinematics eqation we can solve for time.

80 = 0 + (1/2)(10)t²

80/5 = t² = 16

t = 4s

First find the time it takes to reach the top of its path using the equation , where the final velocity is 0m/s, initial velocity is 24m/s, and a is the acceleration due to gravity.  Solve for time (t).

0 = 24 +(-10)t

 t = 2.4s

Notice that this is only the time it takes the object to reach the top of its path, and the question asks for the time it takes the object to reach the ground. In order to find how long it takes to reach the ground simply double this time.

2.4s * 2 = 4.8 s