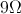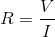All MCAT Physical Resources
Example Questions
Example Question #12 : Capacitors And Dielectrics
A capacitor has a capacitance of 




What is the resistance of the resistor?
The question states that the potential difference dropped from 


This means that there was a 




The time constant, tau, for an RC circuit is the product of the resistance of the resistor and the capacitance of the capacitor:
We can use this equation to solve for the resistance of the resistor:
Solving for resistance gives us:
Notice that you could have used the voltage decay equation to solve this problem; however, knowing the definition of time constant simplifies the problem and reduces the amount of calculations.
Example Question #211 : Electricity And Waves
Which of the following factors would decrease the resistance through an electrical cord?
Increasing the cross-sectional area of the cord
Decreasing the cross-sectional area of the cord
Increasing the resistivity
Increasing the length of the cord
Increasing the cross-sectional area of the cord
The equation for resistance is given by 
From this equation, we can see the best way to decrease resistance is by increasing the cross-sectional area, 


Example Question #211 : Electricity And Waves
An electrician wishes to cut a copper wire 


9.6m
2.6cm
10cm
38m
960m
960m
To relate resistance R, resistivity 

Rearranging to isolate the quantity we wish to solve for, L, gives the equation 
Plugging in our numbers gives the answer, 960m.
Example Question #111 : Circuits
What is the current in a circuit with a 


Resistors in serries add according to the formula:
Resistors in parallel add according to the formula:
We can find the total equivalent resistance:
Now we can use Ohm's law to find the current:
Solve:
Example Question #61 : Ap Physics 2
A 

To find resistance from voltage and current, we will need to use Ohm's law:
We are given the voltage and current, allowing us to solve for the resistance.
Example Question #1 : Molecular Weight, Molecular Formula, And Moles
The atomic mass of lithium is 


The atomic mass of an element is determined by the proportional mass of each elemental isotope. We know that there are only two isotopes of lithium; therefore, their percentages must add to 100%.
The atomic mass will be equal to the mass of each isotope multiplied by its abundance.
We can substitute an algebraic expression to solve for one of our variables.
Using this value, we can solve for the abundance of the other isotope.
Converting these values to percentages gives us our final answer.
Example Question #1 : Molecular Weight, Molecular Formula, And Moles
How many carbon atoms exist in two moles of carbon dioxide?
6.022 * 1023 atoms
1.2 * 1024 atoms
32 atoms
2.7 * 1022 atoms
1.2 * 1024 atoms
It is important to remember that one mole of an element contains 6.022 * 1023 atoms. Since there are two moles of carbon dioxide (CO2), we can conclude that there are two moles of carbon. As a result, there are 
Example Question #3 : Stoichiometry And Analytical Chemistry
A researcher performs an elemental analysis on a compound. He finds that the compound is made up of only carbon, hydrogen, and oxygen atoms. He isolates a pure sample of the compound and finds that this sample contains 






Molecular weight of this compound =
The researcher obtains a sample of 
A mole is defined as the number of atoms present in 


Remember that a mole of any element contains 

Example Question #2 : Stoichiometry And Analytical Chemistry
A researcher performs an elemental analysis on a compound. He finds that the compound is made up of only carbon, hydrogen, and oxygen atoms. He isolates a pure sample of the compound and finds that this sample contains 






Molecular weight of this compound =
When calculating the empirical formula, if you used ratios of the number of atoms of each element instead of ratios of moles of each element, would you get a different answer?
No, because there is a constant relationship between moles and atoms of each element
Yes, because Avogadro’s number is different for each element
Yes, because there is a constant relationship between mass and atoms of each element
No, because the number of moles and the number of atoms in each element is equal
No, because there is a constant relationship between moles and atoms of each element
Remember that the empirical formula relies on the ratio of the moles of elements. To get the number of atoms, you would have to multiply the moles of each element by the Avogadro’s number (
Example Question #5 : Stoichiometry And Analytical Chemistry
Which of the following contains the greatest number of moles?
Each answer choice is presented in grams. To convert to moles, we will need to divide each choice by the atomic mass of the presented element.
Two grams of hydrogen atoms will result in the greatest amount of moles.
Certified Tutor
All MCAT Physical Resources