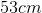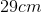All MCAT Physical Resources
Example Questions
Example Question #1 : Torque
One side of a seesaw carries a 

For the seesaw to be balanced, the system must be in rotational equilibrium. For this to occur, the torque the same on both sides.
The total torque must be equal on both sides in order for the net torque to be zero.
Substitute the formula for torque into this equation.
Now we can use the given values to solve for the missing mass.
The acceleration form gravity cancels from each term.
Example Question #1 : Torque
Two masses hang below a massless meter stick. Mass 1 is located at the 10cm mark with a weight of 15kg, while mass 2 is located at the 60cm mark with a weight of 30kg. At what point in between the two masses must the string be attached in order to balance the system?
This problem deals with torque and equilibrium. Noting that the string is between the two masses we can use the torque equation of 


x=43, thus the string is placed at the 43cm mark.
Example Question #1 : Rotational, Circular, And Harmonic Motion
A 2kg mass is suspended on a rope that wraps around a frictionless pulley. The pulley is attached to the ceiling and has a mass of 0.01kg and a radius of 0.25m. The other end of the rope is attached to a massless suspended platform, upon which 0.5kg weights may be placed. While the system is initially at equilibrium, the rope is later cut above the weight, and the platform subsequently raised by pulling on the rope.

The rope is cut just above the 2kg mass, and the platform starts to fall. The rope is still wrapped around the pulley. What is the torque around the pulley?
In the instant the rope is cut right above the 2kg mass, the pulley now has net torque in the counterclockwise direction because the platform with the masses is still connected to the rope that winds around the pulley. Knowing that 
Example Question #1 : Torque
Which of these is the correct expression for torque, τ, when θ is the angle at which the force, F, acts around the axis of rotation?
- τ = F cos θ
- τ = F sin θ
- τ = F tan θ
- τ = F cotan θ
- τ = F sec θ
4
3
5
2
1
2
Choice 2 is correct. Think about trying to change a tire…you apply the force on the tire iron as close to perpendicular as possible in order to generate the most force.
Since the sine of 90 degrees is 1, then you are applying the maximum torque you can generate according to the equation τ = F sin θ.
Example Question #1 : Torque
An attraction at a science museum helps teach students about the power of torque. There is a long metal beam that has one pivot point. At one end of the bar hangs a full sedan, and on the other end is a rope at which students can pull down, raising the car off the ground.
The beam is 40 meters long and the pivot point is 5 meters from one end. A car of mass 500kg hangs from the short end of the beam. Neglecting the mass of the beam, what is the minimum mass of a student who can hang from the rope and begin to raise the car off the ground?
More information is needed to answer
We are trying to find what force needs to be applied to the rope to result in a net of zero torque on the beam.
Torque applied by the car:
We can use this to find the mass of a student that will create the same amount of torque while hanging from the rope:
Example Question #1 : Pendulums
Which of the following changes would increase a pendulum's frequency?
Shortening the length of the pendulum's string
Increasing the length of the pendulum's string
Increasing the angle of displacement
Decreasing the angle of displacement
Increasing the mass at the end of the pendulum
Shortening the length of the pendulum's string
The only two factors that affect a pendulum's frequency are the acceleration due to gravity (g) and the length of the pendulum's string (L). This can be seen in the following formula: 
Example Question #2 : Pendulums
Which factors increase the maximum velocity of a pendulum?
Decreasing both the length of the pendulum's string and the angle of displacement
Increasing both the length of the pendulum's string and the angle of displacement
Increasing the length of the pendulum's string and decreasing the angle of displacement
Decreasing the length of the pendulum's string and increasing the angle of displacement
Increasing both the length of the pendulum's string and the angle of displacement
Both the length of the pendulum's string and the angle of displacement affect the maximum velocity of the pendulum. Increasing the length of the pendulum's string and increasing the angle of displacement both increase the distance the pendulum must travel in a single period, increasing its potential energy at its maximum height, and therefore the maximum velocity at its lowest point.
Example Question #3 : Pendulums
What is the period of a pendulum that has a string length of 9.8m?
The key to answering this question is to recall the following important formula for a simple pendulum: 
Example Question #4 : Pendulums
Which of the following changes to a pendulum will affect the angular velocity?
Decreasing the length of the string
Raising the height from which the mass is released
Increasing the mass on the end of the string
Lowering the height from which the mass is released
Decreasing the length of the string
For a pendulum, the angular velocity is given by the equation 



Example Question #131 : Newtonian Mechanics And Motion
The frequency of a pendulum on Earth is measured to be 
Approximate gravity on moon is 
The frequency of a pendulum is given by the relation ![f \propto \sqrt[\sqrt[]{\frac{g}{L}}{}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/120734/gif.latex)
Since gravity on the moon is one sixth of the gravity on Earth, frequency on the moon will be 
If the frequency on Earth is 

Certified Tutor
Certified Tutor
All MCAT Physical Resources